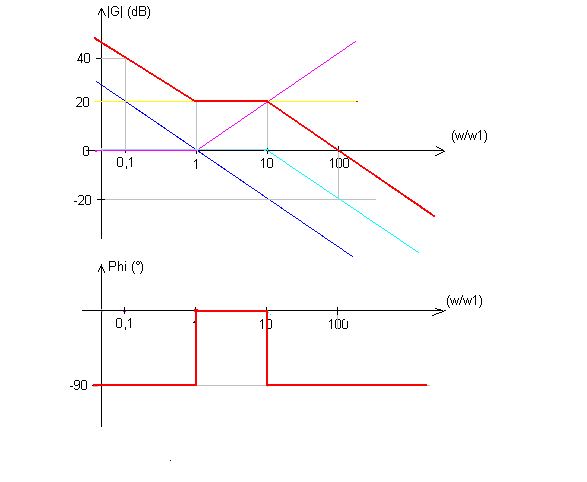
T=1O*(1+jw/w1)/(jw/w1)*(1+jw/W2)  avec w2=10w1


T=1O*(1+jw/w1)/(jw/w1)*(1+jw/(10W1))

Go = 20.log(10) = + 20 dB (en jaune sur le dessin)

(1+jw/w1) : c'est un zéro en w/w1 = 1 --> le gain monte de 20 dB par décade à partir de w/w1 = 1 (en mauve sur le dessin)

1/(jw/w1) : c'est un pôle à l'origine, le gain descent partout à 20 B par décade et sa courbe passe à 0 dB pour w/w1 = 1 (en bleu foncé sur le dessin).

1/(1+jw/(10w1)) : c'est un pole en w/w1 = 10, le gain descent de 20 dB par décade à partir de w/w1 = 10 (en bleu clair sur le dessin)

Pour trouver le |G| (en dB) de l'ensemble, il suffit d'additionner algébriquement les ordonnées des 4 courbes ci-dessus.
On a alors la courbe en rouge (dessin du haut)

(Attention la graduation de l'axe des abscisses est logarithmique de base 10).

Le diagraphe des phases se déduit de celui du gain.

Si la courbe du gain descent à 20.k dB/décade, la phase est de -90.k degrés.
Si la courbe du gain monte à 20.k dB/décade, la phase est de +90.k degrés.
Et si k = 0, le gain est constant et la phase est nulle.

Sauf distraction, vérifie.  

Merci bcp J-P, expliqué comme ca c'est beaucoup plus clair