Inscription / Connexion Nouveau Sujet
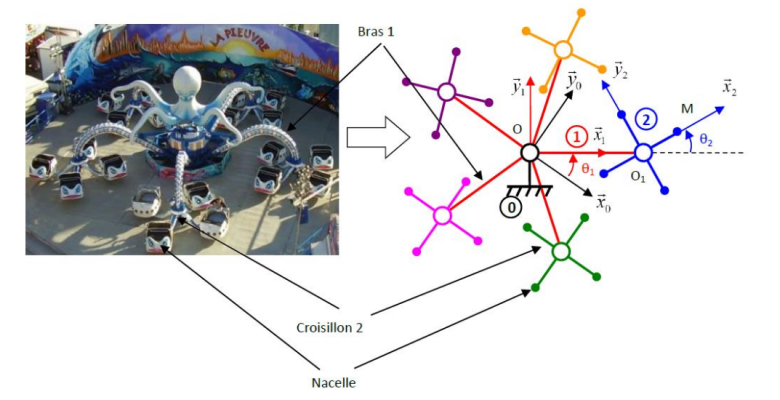
Devoir mécanique 2 la pieuvre
Bonjour , je soumets le deuxième exercice de mécanique.
Hypothèses et données :
8 passagers sont embarqués dans les 4 nacelles du solide 2 (ayant pour masse et centre de gravité
). Le solide 1 a pour masse
et pour centre de gravité
.
1. Exprimer les vecteurs rotation
2. Exprimer la vitesse
3. Exprimer la vitesse
4. Exprimer l'accélération
5. Déterminer le torseur cinétique au point G1
6. Déterminer le torseur cinétique où
au point O
7. Déterminer le torseur dynamique au point G1
J'espère ne pas avoir fait d'erreur de recopie...
Bonjour
Tu peux sans doute donner les résultats. S'il sont bons : tant mieux. Sinon on te demandera d'expliquer ta méthode.
D'accord merci,
cf matrice
Je pense que les deux dernières réponses sont fausses car je viens de voir que je n'ai pas déplacé les points.
Ton énoncé précise bien dans quel repère il faut calculer les différents vecteurs mais il ne précise pas dans quelle base les exprimer... Différentes réponses sont donc possibles.
D'accord avec ton expression de la vitesse de O1 à condition de préciser (ne pas oublier l'indice).
Pas d'accord avec ton expression de la vitesse absolue de M : et
doivent intervenir et les calculs intermédiaires ne doivent pas faire intervenir
qui est un vecteur colinéaire à
. Il faut partir de la relation exprimant le vecteur position et dériver par rapport à t dans Ro :
Les dérivées de vecteurs unitaires s'expriment facilement en faisant intervenir les deux vecteurs rotations définis à la première question.
Pour la vitesse de M on fait comme si il appartenait à En fait on fige la rotation de ( S2)
j'aurais par contre dû écrire
Si je ne me trompe pas...
Figer la rotation de S2 par rapport à S1 pour faire la calcul dans Ro revient à calculer la vitesse d'entraînement de M :
C'est ce que tu obtiens mais à ce vecteur vitesse d'entraînement, il faut ajouter la vitesse relative de M, c'est à dire la vitesse de M par rapport à R1. N'étant pas certain que cette méthode, dite de "composition des vitesses et des accélérations", soit à ton programme, je t'ai proposé la méthode directe... Utilise celle recommandée par ton professeur.
Nous avons effectivement abordé la méthode de composition des vitesses et des accélérations, il nous est cependant conseillé d'utiliser la dérivation de la position (de la vitesse ) considérée plus simple.
Merci pour ton aide et pour le temps investi.
Avec la méthode de dérivation je retrouve bien l'expression de
M étant fixe dans seule la vitesse d'entraînement apparaît.
C'est bien ça ?
Les dérivées de vecteurs unitaires s'expriment facilement en faisant intervenir les deux vecteurs rotations définis à la première question.
les deux vitesses angulaires apparaissent bien dans l'expression de la vitesse de M dans Ro.
Entièrement d'accord si Sinon on tient juste compte de sa position.
Je n'insiste pas, j'ai l'impression de devenir fatiguant.
Encore merci pour ton aide.
Je viens de relire l'énoncé. Il n'est pas précisé que le solide 2 est fixe par rapport au solide 1. Si cela était le cas, on parlerait d'un seul solide et non de deux. Il faut donc a priori considérer l'angle comme une variable. Mais bon : ton professeur a peut-être fourni des indications supplémentaires permettant de considérer
comme une constante. Dans ces conditions, ton calcul serait correct avec
(pas
)
Pour que ce soit clair pour d'éventuels prochains lecteurs , lectrices ( évidemment )
Nous notons en cours avec le symbole
Pour dire : vistesse de M par rapport a comme si il appartenait à 1
Donc comme si (S1) et (S2) étaient soudés mais existe et ne peut être représenté au moment où il coïncide avec
dans le cas général car il s'agit d'un moment particulier.
L'énoncé ne précise pas que (S2) est fixe car (S2) est mobile. Il s'agit d'un simplification ponctuelle pour éviter de trop longs calculs en devoir car le temps est limité.
J'aurais dû le préciser dès le début, je pensais la notation commune.
Je me le note pour la suite.
Bonjour,
Juste une incursion pour une remarque sur la notation commune, avec une équation sous forme d'image pour bien indiquer que c'est une citation d'un cours de cinématique.
On voit bien qu'il y a une vitesse de (), S2 et S1 ne sont pas "soudées".
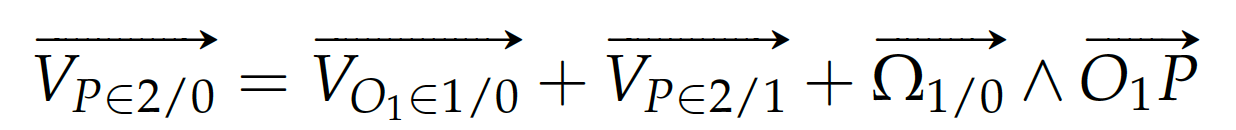
Bonjour gts2 et merci pour cette information qui va dans le sens de mes précédents messages. Les notations utilisées indiquent que le point M est un point fixe de S2. Cela ne veut pas dire que S2 est nécessairement fixe par rapport à S1. Mais bon : quand un étudiant demande confirmation de son travail en étant certain d'avance d'avoir raison, on atteind une limite...


