Inscription / Connexion Nouveau Sujet
deuxième loi de Newton
Bonjour, celaa fait pas mal de temps que je suis sur cet exercice, pourriez vous m'aider à la faire?
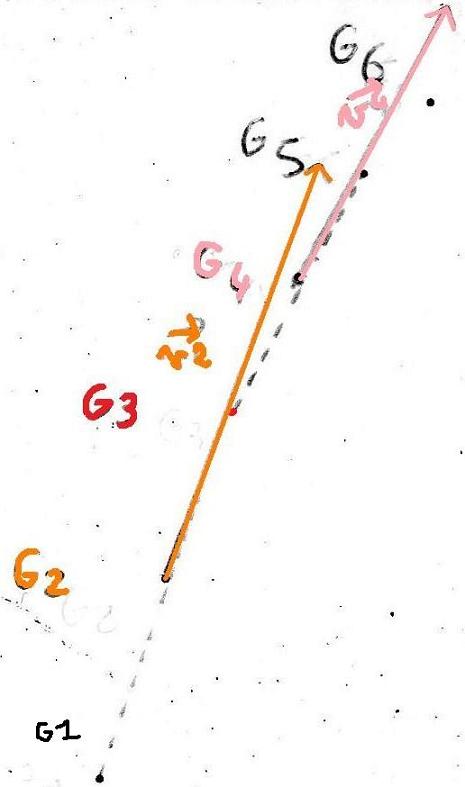
Le document ci joint est une partie du document que j'ai, sinon l'image est trop grande. Ce doc donne les positions successives du centre d'inertie d'un projectile lancé. Les positions successives sont séparées de T= 50ms. L'échelle : 6 cm sur le dessin représentent 50cm.
1cm 1,0m.s^-1
1,0m.s^-1
Au point G3, représenter le vecteur variation de vitesse vect v3= vect4 - vect2, déterminé en additionnant, à partir du point G3, le vecteur v4 et le vecteur -v2. (Faire de même pour tous les autres points).
v3= vect4 - vect2, déterminé en additionnant, à partir du point G3, le vecteur v4 et le vecteur -v2. (Faire de même pour tous les autres points).
Montrer que les tracés sont conformes à cette formulation de la deuxième loi de Newton : "dans un référentiel galiléen, les vecteur variation vitesse du centre d'inertie d'un système et la somme vectorielle des forces subies par ce système sont colinéaires et de même sens.
Je comprends qu'il faut faire partir vect2 de G3, puis au bout de la flèche mettre le vecteur v4 "à l'envers" mais dans quelle direction?
Comment démontrer que les tracés sont conformes à la 2ème loi de Newton?
merci
non attention il faut que tu fasses au point G3 : V4-V2
Donc en ce point tu reportes le vecteur V4 et au bout de la fleche tu traces
-V2.
Ok?
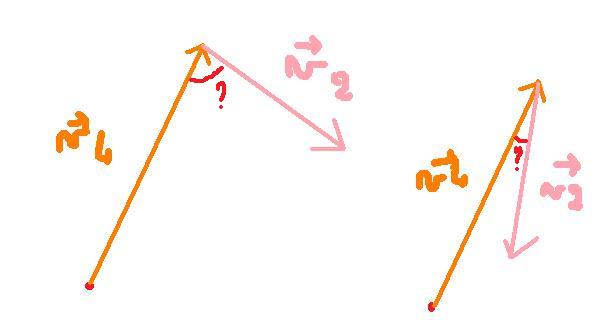
oui ok mais comment savoir quel angle il y a entre v4 et v2?
On peut très bien avoir ces deux situations:
Et comment justifier déontrer que les tracés sont conformes à cette formulation de la deuxième loi de Newton : "dans un référentiel galiléen, les vecteur variation vitesse du centre d'inertie d'un système et la somme vectorielle des forces subies par ce système sont colinéaires et de même sens"?
merci à toi 
Il faut tracer par translation le vecteur v4 en le faisant partir de G3 ,puis à partir de l'extrémité de ce vecteur v4 dessiné ,on trace le vecteur -v2 par translation (il est orienté dans le sens opposé à v2.
Comme il doit s'agir d'un mouvement d'un objet soumis uniquement au poids, on doit avoir le vecteur
v4-v2 vertical vers le bas car le vecteur poids au point A3 est colinéaire et de meme sens que la variation du vecteur vitesse autour de ce point(2ème loi de Newton niveau 1ere S)
Ok.
Le problème est que je dois démontrer que dans un référentiel galiléen, les vecteur variation vitesse du centre d'inertie d'un système et la somme vectorielle des forces subies par ce système sont colinéaires et de même sens (d'ailleurs comment le démontrer?) mais tous les vecteurs variation de vitesse que je trace sur ce schéma ne sont pas colinéaires et qu'est ce que le sens déjà? je confonds avec la direction..
Qu'est ce que a somme vectorielle des forces subies par ce système ?
Merci encore
"Tracés conformes à la 2ème loi de Newton": vecteur v4-vecteur v2 de meme direction et de meme sens que la somme vectorielle des forces extérieures.
S'il s'agit d'un projectile lancé, il est soumis uniquement au poids vertical vers le bas comme la variation du vecteur vitesse qui doit aussi etre aussi vertical vers le bas. Il s'agit d'une vérification et non pas d'une démonstration. De meme, au point G4 la variation des vecteurs v5-v3 doit etre vertical.
Dans le cas de Lulu3324, c'est un mouvement circulaire uniforme avec orientation de la variation du vecteur vitesse vers le centre de la trajectoire.




