Inscription / Connexion Nouveau Sujet
deux masses sur un plan incliné
Bonjour à tous et toutes,
j'ai fait un petit exercice , mais je ne suis pas sûre de ma réponse pour la question 2, si vous pouvez vérifiez svp. merci d'avance.
Voici l'énoncé de l'exercice :
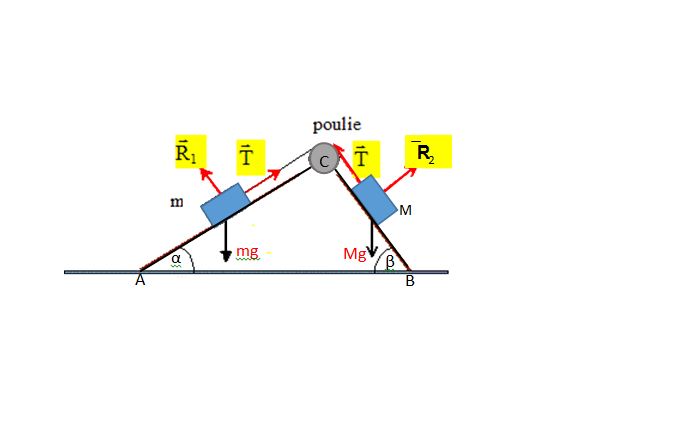
Deux masses m et M sont reliées par un fil inextensible passant sur une poulie parfaite lacée au sommet de deux plan inclinés formant avec le plan horizontal des angles respectifs α et β.
On suppose que les masses peuvent glisser sur les plans inclinés sans frottement.
1. Quelle relation doit exister entre m , M, α et β pour que les système soit en équilibre ?
2. On suppose maintenant que les plans sont rugueux et de même coefficient de frottement f . Quelle doit être la valeur minimale de f pour que le système soit en équilibre ?
3. Calculer f pour m= 3 M , α= 15° et β = 25°
la réponse
R2+Mg+T = 0
R1+mg+T = 0
m.g sin = M.g sinβ
et
T= Mg sinβ ; T= mg sin
La tension dans le câble et la force de la masse forment une paire action-réaction. Puisque la tension est la même pour les deux masses, celles-ci tirent avec la même force .
(vanoise m'a appris beaucoup de choses et parmi lesquelles la réalisation des schéma pour bien comprendre)
La condition d'équilibre donne :
f*mg cosα > mgsinα
f*Mg cosβ> Mgsinβ
𝑓𝑐𝑜𝑠α − 𝑠𝑖𝑛β+ (M/m) = 0 soit 𝑠𝑖𝑛²α(1 + 𝑓²) - (2 M/m)𝑠𝑖𝑛α + (M/m)²- 𝑓² = 0 ;
Bonjour
C'est vrai que tes schémas sont de plus en plus clairs ! Une remarque tout de même : le fil étant de masse négligeable et la poulie étant mobile sans frottement, on peut comme tu l'as fait, considérer les tensions du fil de même norme aux deux extrémités du fil. Cela ne signifie pas que les deux vecteurs forces sont égaux : ils diffèrent par leurs directions. Il serait donc préférables de noter les deux tensions et
pour poser ensuite :
Cela conduit à :
Pour la question 2) il faut commencer par remarquer, avec m=3M :
Sans les frottements, la masse m aurait tendance à descendre la pente, la masse M aurait tendance à monter. Cette remarque permet de déterminer les sens des réactions tangentielles et
exercées par les plans sur les masses. Ensuite il faut écrire les deux conditions d'équilibre en tenant compte de la loi de Coulomb sur les frottements entre solides en absence de glissement.
1)
m.g.sin(alpha) = M.g.sin(Beta)
m.sin(alpha) = M.sin(Beta)
-----
2)
Supposons M à la limite de glisser vers le bas (cas ou M.sin(Beta) > m.sin(beta) ) :
Mg.sin(beta) - T - f * Mg * cos(beta) = 0
T = Mg.sin(beta) - f * Mg * cos(beta
Alors m sera à la limite de glisser vers le haut :
mg.sin(alpha) - T + f * mg * cos(alpha) = 0
T = mg.sin(alpha) + f * mg * cos(alpha)
On a donc : Mg.sin(beta) - f * Mg * cos(beta) = mg.sin(alpha) + f * mg * cos(alpha)
M.sin(beta) - f * M * cos(beta) = m.sin(alpha) + f * m * cos(alpha)
f * (m * cos(alpha) + M * cos(beta)) = M.sin(beta) - m.sin(alpha)
f = (M.sin(beta) - m.sin(alpha))/(m * cos(alpha) + M * cos(beta))
---
Et dans le cas où M.sin(Beta) < m.sin(beta), on trouve par la même méthode :
f = (m.sin(alpha) - M.sin(beta))/(m * cos(alpha) + M * cos(beta))
Donc f min = |m.sin(alpha) - M.sin(beta)|/(m * cos(alpha) + M * cos(beta))
avec m = 3M, alpha = 15° et Beta = 25° -->
f min = |3M.sin(15°) - M.sin(25°)|/(3M * cos(15°) + M * cos(25°))
f min = |3.sin(15°) - sin(25°)|/(3 * cos(15°) + cos(25°))
f min = 0,093
-----
Sauf si je me suis planté. 
bonjour tout le monde
je vous remercie énormément pour votre aide...
Un rappel :
Les forces de frottements s'opposent toujours au mouvement.
si on a un déplacement selon + X , la force tangentielle de frottement sera orientée selon - X , et on aura donc:
Rt1= -f Rn X
et pareil pour Rt2
en présence de frottements, si le glissement entre les solides est nul , alors il existe entre les composantes normale et tangentielle de l'effort de contact la relation  T
T /
/  N
N < f
< f
et si les deux solides glissent l'un par rapport à l'autre cela devient :
 T
T /
/  N
N = f
= f
Bonjour nano21
En utilisant les résultats que tu viens de rappeler, tu devrais tout seul être capable d'obtenir l'inégalité vérifiée par le coefficient de frottement.
Remarque : je ne sais pas si ton professeur fait la différence entre coefficient de frottement statique et coefficient de frottement dynamique. Rigoureusement, en absence de glissement :
T / N  fs : coefficient de frottement statique
fs : coefficient de frottement statique
existence d'un glissement : T / N = fd : coefficient de frottement dynamique.
En pratique : fs>fd mais l'écart entre les deux coefficients est de l'ordre de 10%. Parfois, pour simplifier, on ne fait pas la différence entre les deux coefficients en les considérant comme identiques.C'est peut-être ce que fait ton professeur.
Sinon, ton énoncé est clair : il s'agit d'étudier la condition d'équilibre donc l'absence de glissement comme expliqué dans mon message du 19-06-17 à 16:53. C'est donc le coefficient de frottement statique qui intervient.
bonjour Vanoise,
Merci pour ces explications vraiment claires comme de l'eau de source.. ...je te souhaite excellentes journée.
...je te souhaite excellentes journée.
bonjour j-p,
je voulais te remercier encore une fois, j'ai analysé attentivement ton raisonnement , il est correcte... .Très bonne journée à toi!
Bonjour nano21
Si ton professeur ne fait pas la différence entre coefficient de frottement statique et coefficient de frottement dynamique, il acceptera le raisonnement précédent. A titre documentaire, voici l'étude de l'équilibre, donc l'étude de l'absence de glissement. Puisque : , l'absence de glissement suppose une réaction tangentielle
orientée vers le haut de la pente et une réaction
orientée vers le bas. Je note
et
les deux réactions normales. Inutile je pense de refaire le schéma.
Condition d'équilibre de la masse m :
En projetant sur deux axes orthogonaux respectivement colinéaire et orthogonal à la ligne de plus grande pente et en notant T la valeur commune :
Étude analogue de l'équilibre de la masse M :
En éliminant T entre (1) et (3) on obtient :
Loi de Coulomb sur l'absence de glissement entre solide :
Addition membre à membre des relations (6) et (7) :
Soit, en tenant compte de (2) et (4) :
En remplaçant dans (5) et en simplifiant par g, on obtient l'inégalité vérifiée par le coefficient de frottement statique en absence de glissement :


