Inscription / Connexion Nouveau Sujet
Accueil l'île de la physique - chimie Forum de physique - chimieListe de tous les forums de physique - chimie SupérieurOn parle exclusivement de physique/chimie, pour le supérieur principalement, les BTS, IUT, prépas... LicenceForum Supérieur de licence PhysiqueTopics traitant de Physique [tout]Lister tous les topics de physique - chimie
Niveau licence
Partager :

Deux masses et un ressort

Posté par
saba70 23-02-16 à 14:14

Bonjour à tous, dans un exercice de mécanique je dois étudier le mouvement de deux masses accrochées à un ressort, sur l'axe horizontal.
- On me demande en premier d'exprimer la variation x de longueur du ressort par rapport à sa position d'équilibre ! Je trouve x=x2-x1-l
x2=position de la masse 2 par rapport à l'origine
x1=position de la masse 1 par rapport à l'origine
l =la distance entre les deux masses à l'équilibre.
-on me demande ensuite d'établir les équations différentielles vérifiées par x1 et x2, puis celle de x.
Je trouve : x(..)=(-k*x)/m2 - (k*x)/m1
m2 et m1 les masses respectives des masses 2 et 1.
Est ce que c'est juste déjà ?
Le problème c'est que dans cette même question on me dit : "on écrira l'équ. diff de x sous la forme x(..) + (k/)*x=0, étant la masse réduite du systeme dont on calculera l'expression". Ce chapitre est nouveau et je ne comprends pas trop comment faire..
J'espere que vous pourrez m'aider, merci.

Posté par
vanoisere : Deux masses et un ressort 23-02-16 à 14:31

Bonjour

OK pour le début. Ensuite RFD appliquée à chaque masse puis soustraction "membre à membre" :

\begin{cases} \\ m_{2}\cdot \ddot{x}_{2}=-k\left(x_{2}-x_{1}-l\right) & \ddot{x}_{2}=-\frac{k}{m_{2}}\cdot x\\ \\ m_{1}\cdot\ddot{x}_{1}=k\left(x_{2}-x_{1}-l\right) & \ddot{x}_{1}=\frac{k}{m_{1}}\cdot x\\ \\ \ddot{x}=\ddot{x}_{2}-\ddot{x}_{1} & \ddot{x}=-k\cdot\left(\frac{1}{m_{1}}+\frac{1}{m_{2}}\right)\cdot x \\ \end{cases}

Posté par
vanoisere : Deux masses et un ressort 23-02-16 à 14:31

Bonjour

OK pour le début. Ensuite RFD appliquée à chaque masse puis soustraction "membre à membre" :

\begin{cases} \\ m_{2}\cdot \ddot{x}_{2}=-k\left(x_{2}-x_{1}-l\right) & \ddot{x}_{2}=-\frac{k}{m_{2}}\cdot x\\ \\ m_{1}\cdot\ddot{x}_{1}=k\left(x_{2}-x_{1}-l\right) & \ddot{x}_{1}=\frac{k}{m_{1}}\cdot x\\ \\ \ddot{x}=\ddot{x}_{2}-\ddot{x}_{1} & \ddot{x}=-k\cdot\left(\frac{1}{m_{1}}+\frac{1}{m_{2}}\right)\cdot x \\ \end{cases}

Posté par
vanoisere : Deux masses et un ressort 23-02-16 à 14:33

Désolé : beug du serveur du forum ou erreur de manipulation de ma part ? Le message  apparaît en double exemplaire !

Posté par
saba70re : Deux masses et un ressort 23-02-16 à 19:55

Merci beaucoup, la masse réduite est donc m1 + m2 c'est ça ?
Une dernière question demande de comparer la période T des oscillations du système aux périodes T1 et T2 obtenues lorsque respectivement m1 et m2 sont à l'extrémité du ressort, l'autre extrémité étant fixe. Je ne comprends pas trop cette question ..

Posté par
vanoisere : Deux masses et un ressort 23-02-16 à 21:24

Citation :
Merci beaucoup, la masse réduite est donc m1 + m2 c'est ça ?

Non ! réfléchis :

\frac{1}{m_{1}}+\frac{1}{m_{2}}=\frac{1}{\mu}\quad donc\quad\boxed{\mu=\frac{m_{1}\cdot m_{2}}{m_{1}+m_{2}}}

Posté par
saba70re : Deux masses et un ressort 23-02-16 à 22:30

Oui exact merci, j'avais pas fait attention au fait qu'il fallait mettre les fractions au même dénominateur.

Posté par
saba70re : Deux masses et un ressort 23-02-16 à 23:09

Par contre je ne comprends pas comment il faut faire avec les périodes..

Posté par
vanoisere : Deux masses et un ressort 23-02-16 à 23:24

Je n'ai pas l'énoncé mais a priori, une équation différentielle de la forme :

\ddot{x}+\frac{k}{\mu}\cdot x=0
admet une solution sinusoïdale de la forme :

x=X_{m}\cdot\cos\left(\omega\cdot t+\varphi\right)
de pulsation :

\omega=\sqrt{\frac{k}{\mu}}
et de période :

T=\frac{2\pi}{\omega}=2\pi\cdot\sqrt{\frac{\mu}{k}}
Je te laisse faire la démonstration (très facile...)

Posté par
saba70re : Deux masses et un ressort 24-02-16 à 00:20

Je trouve en remplacant : T = 2*(m1*m2)/k(m1+m2))
ça c'est bien la période des oscillations du système ? Pour les autres périodes on utilise la formule 2*(m/k) ; avec m la masse ?

Posté par
vanoisere : Deux masses et un ressort 24-02-16 à 10:43

Bonjour

Citation :
ça c'est bien la période des oscillations du système ?

Oui !

Posté par
saba70re : Deux masses et un ressort 24-02-16 à 11:26

je ne comprends pas quand ils disent "m1 et m2 sont à l'extrémité du ressort", ça veut dire que m1 et m2 sont serrés au maximum ? Merci beaucoup pour votre aide..

Posté par
vanoisere : Deux masses et un ressort 24-02-16 à 12:46

Citation :
je ne comprends pas quand ils disent "m1 et m2 sont à l'extrémité du ressort"

Dans ces conditions, beaucoup de choses ont dû t'échapper ...
Voici un schéma possible : sans garantie, n'ayant pas l'énoncé complet.
Les orientations des vecteurs forces T1 et T2 sont valides si le ressort est allongé par rapport à sa longueur à vide : x2 - x1 > l avec l : longueur à vide.
Pour x2-x1 <l, il faudrait inverser les sens des deux vecteurs forces.

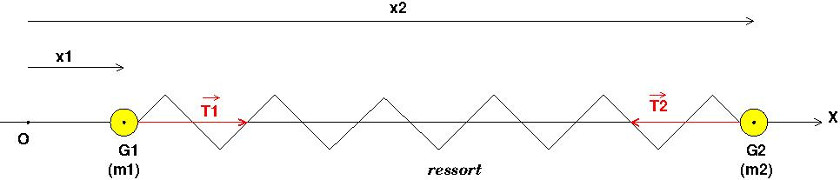
Deux masses et un ressort

Posté par
saba70re : Deux masses et un ressort 24-02-16 à 17:39

Oui j'ai bien le même schéma sur mon énoncé mais je ne vois pas le rapport avec les périodes..

Posté par
vanoisere : Deux masses et un ressort 24-02-16 à 19:27

Imagine que tu écartes les deux masses de façon à avoir (x2-x1)>l et qu'alors tu abandonnes le système à lui-même : tu vas bien observer des oscillations : le ressort va se comprimer puis se détendre de façon périodique : les points G1 et G2 vont être animés de mouvements sinusoïdaux. Ces mouvements sont périodiques.
En pratique, il faut imaginer deux grosses perles enfilées sur une tige horizontale fixe par rapport à la terre, le ressort reliant les deux perles entourant la tige. Les perles sont supposées mobiles sans frottement et la masse du ressort est supposée négligeable devant m1+m2.

Posté par
saba70re : Deux masses et un ressort 24-02-16 à 21:05

Ah d'accord je vois, si j'ai bien compris ça veut dire que G1 et G2 ont les mêmes oscillations et ont donc la même période ?

Posté par
vanoisere : Deux masses et un ressort 24-02-16 à 22:29

Pour démontrer ce que tu viens d'écrire, il faut partir de l'expression de x qui a été démontrée précédemment et d'autre part remarquer que les deux premières égalités de mon message du   23-02-16 à 14:31 conduisent à :
m_{2}\ddot{x}_{2}+m_{1}\ddot{x}_{1}=0
En intégrant et en considérant les deux vitesses initiales nulles :
m_{1}\dot{x}_{1}+m_{2}\dot{x}_{2}=0
En intégrant une nouvelle fois par rapport au temps :
m_{1}x_{1}+m_{2}x_{2}=m_{1}x_{10}+m_{2}x_{20}
les indices "o" correspondent à l'instant initial.
Avec :
x=X_{m}\cdot\cos\left(\omega\cdot t+\varphi\right) =x_2-x_1 -l
tu obtiens un système de deux équations à deux inconnues .

Posté par
saba70re : Deux masses et un ressort 28-02-16 à 22:38

D'accord merci, je vais essayer de me debrouiller, bonne soirée et merci encore


Rechercher
Menu
Espace membre
Changer d'île
Mentions légales - Retrouvez cette page sur l'île de la physique - chimie
© digiSchool 2025

Vous devez être membre accéder à ce service...

Pas encore inscrit ?

1 compte par personne, multi-compte interdit !

Ou identifiez-vous :

Rester sur la page

Désolé, votre version d'Internet Explorer est plus que périmée ! Merci de le mettre à jour ou de télécharger Firefox ou Google Chrome pour utiliser le site. Votre ordinateur vous remerciera !