Inscription / Connexion Nouveau Sujet
Déterminer l'inductance et la capacité sur un enregistrement
Salut à tous,
J'ai un exercice en physique qui me pose problème !
Voici l'énoncé :
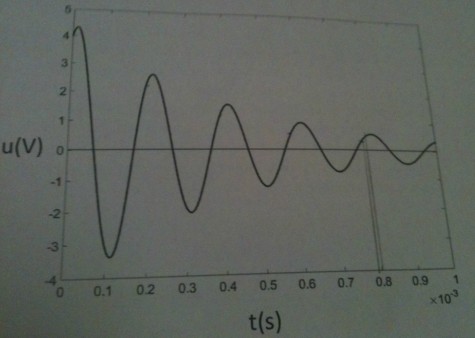
On a enregistré la tension aux bornes d'un condensateur, dans un circuit RLC série. La résistance est de 5  .
.
Déterminer les valeurs de l'inductance L et de la capacité C.
******************************************************
On sait que on est dans le cas d'un regime pseudo périodique.
Ensuite j'ai cherché la période T, tel que T : 2  10 -4s
10 -4s
Or comme on est dans le cas d'un regime pseudo périodique,
Mais là je me rend compte que ça ne va pas... Je sais que je doit utiliser la valeur de la résistance ! Mais comment ?
Merci d'avance, et bonne fête !
Bonsoir,
J'imagine que tu es capable d'écrire l'équation différentielle vérifiée par u(t) et que tu connais l'expression générale de sa solution dans le cas d'un régime pseudo périodique.
Tu as deux inconnues L et C. Tu as donc besoin de deux équations tirées de l'examen de la courbe. La première est l'expression de la pseudo période.
La seconde concerne l'amortissement. Plusieurs méthodes plus ou moins précises sont possibles. La plus précise à mon avis concerne la détermination du décrément logarithmique. As-tu étudié cette notion ? Si oui, tu peux le déterminer graphiquement puis l'exprimer en fonction des caractéristiques du circuit. R apparaît effectivement dans l'expression...
Salut Vanoise et merci de ta réponse 
Pour l'équation différentielle, je l'établie en Uc ?
Du coup d'après la loi des mailles on a :
UC + UR + UL =0 [...]
Avec et
Dans le cas d'un régime pseudo-périodique, on a pour solution générale : ( je ne remontre pas tout les calculs avec  ...)
...)
Je ne comprend pas pourquoi, on utilise ces équations là ?
Non, je n'est pas vu la notion de décrément logarithmique ...
Bonjour,
OK pour ce que tu as fait. p est une valeur négative dépendant de R, L et C.
Tu peux mesurer graphiquement la valeur de u(t) du premier maximum : Um(t1)
Tu peux mesurer graphiquement la valeur de u(t) du maximum suivant : Um(t1+T)
Tu peux en déduire le logarithme du rapport :
A partir de l'équation u(t) que tu as écrite, tu peux exprimer la valeur théorique de  en fonction de p et T.
en fonction de p et T.
Tu en déduiras la valeur de p. Connaissant p et T, tu pourras déterminer L et C.
Ton enregistrement est un peu déformé par la photocopie. Ne ressemblerait-il pas par hasard à celui-ci ?
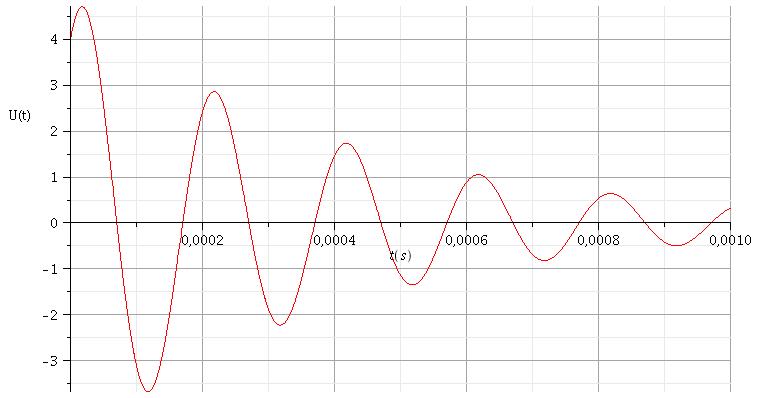
RLC série pseudo oscillatoire :
d²u/dt² + (R/L).du/dt + u/(LC) = 0
p² + (R/L).p + 1/(LC) = 0
p = [-(R/L) +/- i.racinecarrée(4/(LC) - R²/L²)]/2
p = -R/(2L) +/- i.racinecarrée((4L-R²C)/(4L²C))
coeff d'amortissement = -R/(2L)
Constante de temps d'amortissement = 2L/R
On mesure sur le dessin : 2L/R = 0,41.10^-3 s (environ, dessin distordu)
--> 2L = 0,41.10^-3 * 5
L = 1 mH
C par la pseudo période ...
-----
Sauf distraction. 
Salut à tous et merci de vos explications, je comprend vraiment mieux !
Désolé d'avoir mis tant de temps à répondre également ^^
Oui, en effet, mon enregistrement ressemble bien à ça !
*Vanoise, je suis désolé, mais je ne comprend pas du tout à quoi correspond  , et comment l'utiliser... en fait pour trouver Um (t1) et Um (t1+ T) c'est ok, mais par contre comment je fais le lien avec le reste ?
, et comment l'utiliser... en fait pour trouver Um (t1) et Um (t1+ T) c'est ok, mais par contre comment je fais le lien avec le reste ?
*J-P, juste je ne comprend pas comment tu a trouvé " " (la constante de temps d'amortissement", sur l'enregistrement ?
" (la constante de temps d'amortissement", sur l'enregistrement ?
Encore merci de vos aide : )
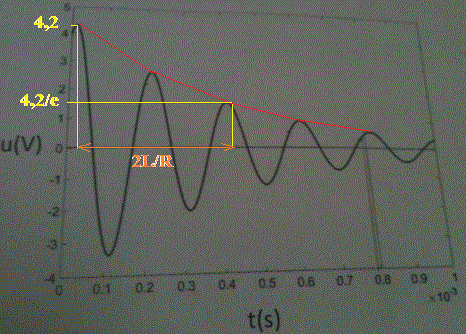
On trace une exponentielle passant par tous les maxima de la sinusoïde amortie (en pratique, on est un poil plus loin que les maxima pour les points où l'exponentielle rencontre la sinusoïde amortie, mais c'est de tellement peu que cela n'influence pas significativement les résultats).
C'est la courbe que j'ai dessinée en rouge.
La courbe en rouge est l'image de la fonction f(t) = e^(-t.R/(2L)) ... dont la constante de temps vaut tau = 2L/R (dans le cas du RLC série dont il est question dans l'énoncé)
En mesurant cette constante de temps sur le graphe ... on obtient la valeur de 2L/R.
Pour ce faire :
On part d'un point de cette courbe en rouge et on note son ordonnée y1 (par exemple, j'ai pris le point d'ordonnée y1 = 4,2 et son abscisse est t1
On trace une parallèle à l'axe des abscisses d'équation y = y1/e (avec e = 2,718281... la base des log népériens)
Cette droite coupe la courbe en rouge à un instant t2, et on mesure sur le dessin : (t2 - t1) qui est égal à tau = 2L/R (en orange sur mon dessin)
Remarque ; on peut prendre, comme point de départ sur la courbe rouge, un autre point de la courbe en rouge que celui que j'ai pris ... on aura le même résultat pour la valeur de 2L/R.
Mais, il vaut mieux choisir comme point de départ, un point de grande ordonnée, cela diminue les imprécisions dues au dessin.
Sauf distraction. 
Bonsoir,
C'est bien de ta part de vouloir approfondir...
Première remarque : faire intervenir le facteur de qualité peut présenter des avantages en régime sinusoïdal forcé mais présente peu d'intérêt ici (trop de fractions à manipuler...). Il est préférable de l'écrire sous la forme :
et comme tu l'as défini. Tu peux montrer facilement que pour
le régime est pseudo périodique avec une solution de la forme :
Avec une pseudo-pulsation :.
La méthode, à mon avis, la plus précise consiste à mesurer les maximums successifs de la tension :.
Soit la date du premier maximum :
; la date du second maximum est
, la date du Nième maximum est
, etc... On obtient donc:
On passe au logarithme :
La méthode consiste à mesurer les valeurs successives des maximums puis à représenter graphiquement les variations de
en fonction du numéro N du maximum.
Cette méthode a deux avantages :
1° : le fait d'obtenir des points sensiblement alignés constitue une vérification expérimentale de la théorie qui a conduit à un amortissement exponentiel au cours du temps :
2° : le coefficient directeur de la droite vaut :
; un programme de régression linéaire permet d'obtenir une valeur de relativement précise puisque l'influence des erreurs aléatoires commises sur la détermination des valeurs des maximums successifs est fortement atténuée par le programme et par le nombre assez élevé de mesures.
On obtient une valeur de voisine de 0,5, ce qui conduit à une valeur de L de l'ordre de 1mH. Puisque :
:
La valeur de C est de l'ordre de 1µF.
La valeur absolue de la pente est appelé ” décrément logarithmique ”. Je te laisse démontrer qu'il s'agit aussi de :
Cela dit, cette méthode est vraiment intéressante si l'enregistrement de la courbe u=f(t) est obtenue à l'aide d'un oscilloscope numérique où d'une carte d'acquisition piloté par un logiciel ; les mesures des maximums successifs sont alors relativement précises. Dans le contexte de ton exercice, la méthode présentée par J.P. consistant à choisir seulement deux points peut suffire.
Remarque : est homogène à une pulsation donc à l'inverse d'un temps. Il est donc possible de définir une constante de temps :
.
Encore merci de vos aides ^^
* J-P, d'accord je comprend mieux, merci de toute tes explications !
* Vanoise, merci de m'avoir expliqué cette méthode, je pense avoir bien compris ce qu'il fallait faire, ça pourra m'être utile, j'ai un contrôle à la rentré sur ce chapitre ^^
Je vais essayer de refaire les calculs, pour voir si j'ai bien tout compris !
En tout cas, encore merci à vous deux pour vos aides ; )


