Niveau licence

Détermination du mouvement d'un objet

Posté par
sido21 06-12-15 à 12:21

Bonjour,

Je n'arrive pas du tout à trouver comment résoudre ce problème :
Une balle initialement au repos et accélérée de manière constante sur une distance de 2m atteint une vitesse de 40m/s. Que vaut l'accélération à laquelle elle a été soumise ?

J'ai commencé par écrire x(t), v(t) et a(t), mais ensuite je suis coincée.

Merci d'avance pour votre aide.

Posté par re : Détermination du mouvement d'un objet 06-12-15 à 12:42

Salut,

Etat initial :
x(0) = 0
v(0) = 0
--> balle initialement au repos.

Pendant une durée, $\Delta t$ , la balle part de 0 m, 0 m/s pour atteindre une distance $d = 2~ m$ à $v = 40 ~m/s$ .

donc $\Delta t = \dfrac{d}{v} = \dfrac{2}{40} = 0,05~ s$

Ensuite, si on regarde ceci sur un graphe :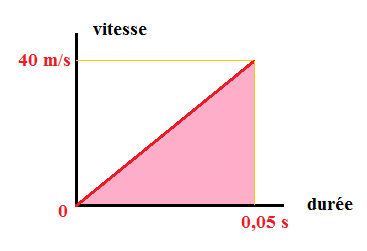
$Détermination du mouvement d\'un objet$
Que vaut l'accélération ?

Posté par re : Détermination du mouvement d'un objet 06-12-15 à 13:39

Merci beaucoup !!

La pente de la courbe de la vitesse correspond à l'accélération donc a = 40/0.05 = 800 m/s2

Posté par re : Détermination du mouvement d'un objet 06-12-15 à 13:40

Bonjour gbm,
t'es sur de toi là?
Ne traites-tu pas une vitesse constante lorsque tu écris t=d/v?

Posté par re : Détermination du mouvement d'un objet 06-12-15 à 13:44

J'écris t=v/a
et
x=(1/2)at²=(1/2)v²/a
donc a=v²/2x=1600/4=400ms^-2 et t=0,1s
Non?

Posté par re : Détermination du mouvement d'un objet 06-12-15 à 14:41

Bonjour sanantonio312, merci pour ton alerte .

Effectivement j'ai commis une erreur d'hypothèse à la base (ça m'apprendra à vouloir répondre trop vite ) ...

Etat initial :
x(0) = 0
v(0) = 0
--> balle initialement au repos.

Pendant une durée, $\Delta t$ , la balle part de 0 m, 0 m/s pour atteindre une distance $d = 2~ m$ à $v = 40 ~m/s$ .

donc

$\dfrac{d^2x}{dt^2} = a \\ \Leftrightarrow \dfrac{dx}{dt} = a \times t + v(0) = a.t = v \\ \Leftrightarrow x(t) = \dfrac{1}{2} \times a \times t^2 + x(0) = \dfrac{1}{2}.a.t^2$

dans ces conditions, à $t = T$ (dès qu'on atteint la distance d = 2 m) :
$d = \dfrac{1}{2} \times a \times T^2 \\ \Leftrightarrow d = \dfrac{1}{2} \times a \times (\dfrac{v}{a})^2 = \dfrac{1}{2}.\dfrac{v^2}{a} \\ \\ \Leftrightarrow \boxed{a = \dfrac{v^2}{2d} ~et~t=\dfrac{v}{a}}$

Désolé pour la faute d'inattention !