Inscription / Connexion Nouveau Sujet
Densité linéique-surfacique-volumique
Salut à tous , j'ai un exo que j'ai pas très bien compris , voilà :
Soit un fil fin de centre O, dirigé suivant un axe Oz, de longueur 2L et portant une charge électrique totale Q répartie linéairement.
1) Donner l'expression de la densité lineique de charge moyenne λm
si on suppose que la répartition est uniforme.
2)Cette distribution de charge n'est pas uniforme et suit la loi :
λ(z)=λo cos(πz/2L) pour -L≤Z≥L et λ(z)=0 pour |z|≥L
Exprimer la charge elementaire dQ située en z sur une portion de fil dz.En déduire l'expression de λo en fonction de Q et L.
Même la question 1 est un peu flou pour moi😢
Bonjour,
J'ai une charge Q = 2 C répartie uniformément sur une longueur de 2 m
Quelle est la densité linéique, càd le nombre de C par m ? (c'est une simple règle de 3)
Ici on a une charge Q uniformément répartie sur une longueur 2L donc 
m = ....
Même type de raisonnement pour une densité surfacique / volumique de charges, sauf que l'on obtient alors respectivement des C/m2 ou des C/m3.
Bonjour à vous deux,
@ Tatsuya23 : pourrais-tu mettre à jour ton profil :
ESPACE MEMBRE / clique sur ton pseudo / MON COMPTE / Mon Profil
Bonjour gbm,
oui,
m=Q/(2L) en C/m
moi c'est le terme "moyenne" qui me derange , je voudrais connaître sa signification
C'est la meme signification que lorsqu'on parle de vitesse moyenne sur un trajet.
Ici,
m est la charge moyenne par unite de longueur.
Et la densite lineique reelle
vaut m (en tout point du fil) uniquement si la repartition de la charge est uniforme.c'est ce dont j'avais pensé aussi merci.
Pour la suite de l'exercice j'arrive pas à comprendre aussi voilà :
3) En s'approchant de l'axe Oz, le fil apparaît comme un cylindre d'axe Oz et de rayon R. On considère alors que la charge est répartie en surface. Sachant que pour un z fixé et sur une hauteur dz, la répartition est uniforme, exprimer,comme au 2), la charge élémentaire dQ située en z sur une hauteur dz. En déduire l'expression de la distribution surfacique de charge σ(z) en fonction de λo, L et z puis en fonction de Q,L et z.
Comme expression de λo j'avais eu πQ/4L
3) par def. dQ = 
(z) dS
dS etant la surface de la portion elementaire de cylindre hachuree sur le dessin:
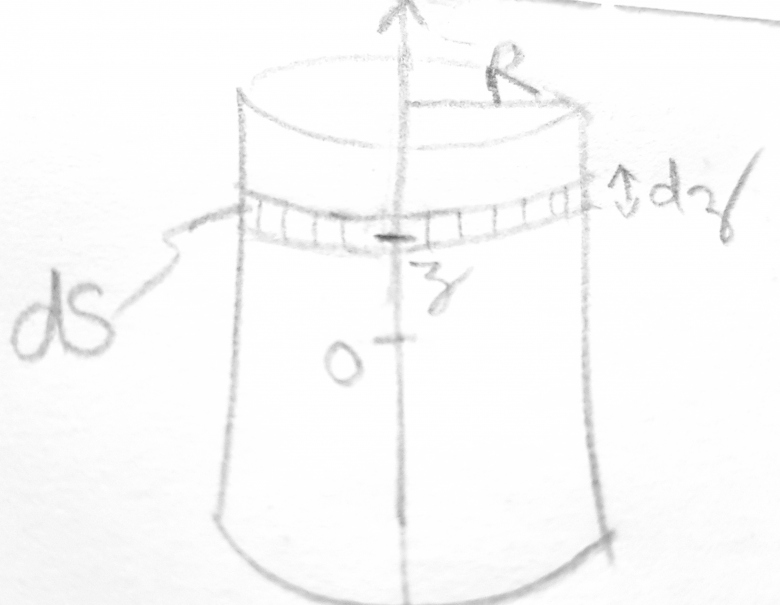
Le dQ je l'avais trouvé
Donc maintenant si on fait l'integral de surface on aurait Q = σ(z) × surface
et la surface = 2πRdz ?
Attention, depend ici de z
Q = 
dS
et ici on trouve:
Q = -L L 2
R (z) dz
Et on obtient (z) en ecrivant que la charge contenue entre z et dz vaut celle de la question 1)
donc dQ = dS = o .....
Et on obtient
(z) en ecrivant que la charge contenue entre z et dz vaut celle de la question 2
.....
J'arrive toujours pas à faire ça .
Pourquoi ça vaut celle de la Q2 ?
Et la condition -L≤z≥+L n'est pas juste valable dans le cas où c'est pas uniforme ???
En plus dans mes expressions finales,R apparait toujours alors qu'on m'a demandé en fonction de lambda 0 , L et z 😔
je comprends l'énoncé comme suit:
dans le 2) on avait une densite lineique (z), donc sur une portion de fil de hauteur dz, dQ=(z) dz
3)Maintenant on suppose que l'on a un fil cylindrique, avec une densite surfacique (z) : donc cette meme portion de fil porte dQ = dS = (z) dz ce qui donne par identification
Annuler
connectez vous