Inscription / Connexion Nouveau Sujet
Démonstration Mécanique (Physique)
Bonjour à tous,
Je suis en deuxième année d'IUT Génie Civil et j'ai une question à vous poser à propos d'un de mes cours de mécanique des sols. Je sais ce n'est pas de la physique à proprement parler mais la question que je me pose est une question mathématique et non pas directement liée au cours de méca sol.
Je ne parviens pas à refaire la démonstration qui est sur cette diapo jointe de mon cours. Est-ce quelqu'un pourrait me détailler et m'expliquer les étapes de calcul svp. J'ai quelques lacunes en maths du coup cela me pose problème pour refaire cette démo encadrée: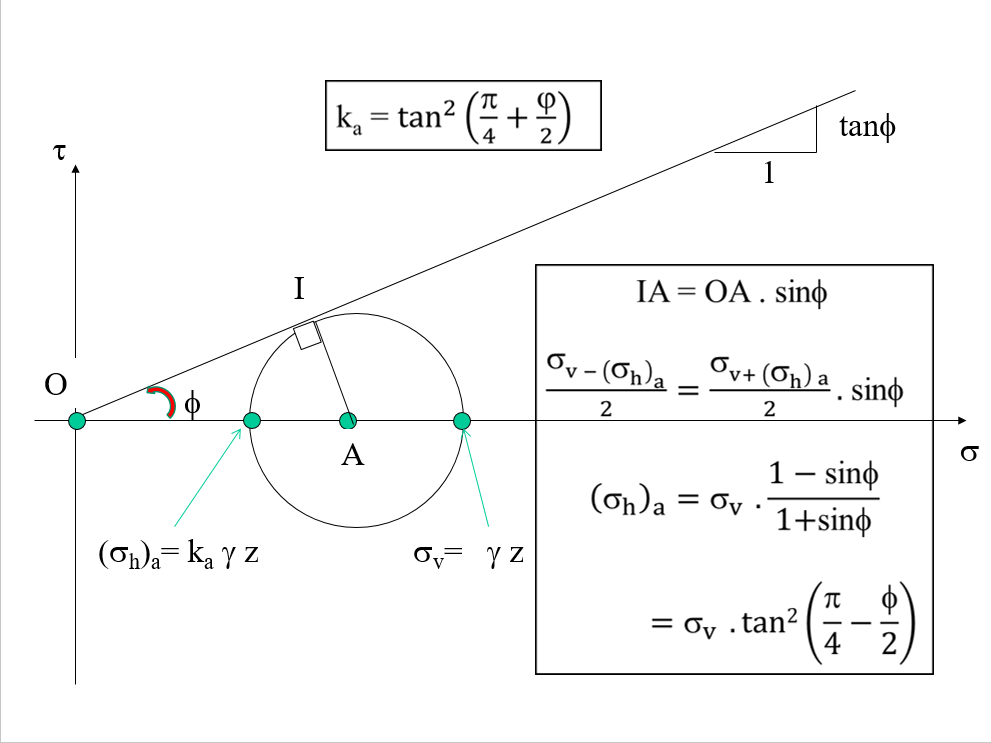 [/url]
[/url]
Merci pour vos futures réponses, cordialement.
----------------------
***Image toléré cette fois-ci mais il faudra recopier les formules la prochaine fois !***
Bonjour,
Je suppose que cela coince au niveau trigo.
1- transformer sin(x) en cos( ...x ...) (ceci pour faire apparaitre le
2- transformer les 1+cos et 1-cos en sin/cos d'angle moitié (ceci pour faire apparaitre le )
3- vous devriez voir apparaitre votre tan2
Bonjour
- La deuxième ligne de l'encadré est juste une repetition de la premiere. En effet :
i.
σv = (σh)a + diamètre du cercle
=> (σv - (σh)a) = (diamètre du cercle)/2 = Rayon = IA
ii. (σv + (σh)a) / 2 : c'est la moyenne arithmétique. C'est donc la distance de O au milieu des deux bouts. C'est donc la distance de O au centre du cercle :
(σv + (σh)a) / 2 = OA
- La troisième ligne provient de l'équation de la deuxième ligne :
i. se débarrasser de la division par 2 des 2 côtés de l'équation
ii. on regroupe les termes en σv d'un côté et en σh)a de l'autre :
(σh)a sin Φ + (σh)a = σv - σv sin Φ
(σh)a (1 + sin Φ) = σv (1 - sin Φ)
=> (σh)a = σv * (1 - sin Φ) / (1 + sin Φ)
- La quatrième ligne est un rappel de ce qui apparaît sur la figure :
(σh)a = ka * γ * Z
σv = γ * Z
Ainsi : (σh)a = σv * ka
Mais là, il y a confusion entre l'angle φ et l'angle Φ...
Bonjour à vous deux,
@kongzi : tout comme sur îlemaths, il n'est pas interdit d'intervenir sur un sujet déjà pris en charge, à la condition de respecter les règles de bienséance.
En l'occurrence ici, gts2 avait déjà donné des éléments de réflexion et attendait un retour de Sevanhugo pour poursuivre l'échange.
Ensuite, on ne fournira pas des solutions toutes faites ...
Merci donc d'y faire attention car ce sont deux motifs d'avertissement sur les 3 
Bonjour
@gbm
C'est vrai que j'ai une mauvaise tendance au zèle dans l'assistance. Mais a ma décharge :
1. Rien de ce que j'ai écrit n'interfère avec la contribution de @gts2 (c'est ce qui me semblait du moins)
- ma contribution certes trop détaillée concernait uniquement les aspects mathématiques
Quoi qu'il en soit, j'ai pris note de devoir changer ma manière d'assister.
Certes, il aurait été préférable d'attendre la fin de l' échange pour proposer éventuellement des compléments mathématiques.
En l'absence de retour de Sevanhugo, difficile de savoir ce qu'il en aurait été.
Je te remercie donc d'en tenir compte les prochaines fois.
Bonne journée à vous tous, 
Bonjour à tous,
Excusez-moi pour ma réponse tardive.
J'ai lu toutes vos réponses et je vous remercie d'avoir pris le temps de m'aider. Je dois avouer que bien que trop détailler pour la charte du site, la réponse de kongzi m'a été très utile.
J'ai pu me poser et refaire tranquillement la démo et retomber sur les calculs de mon cours. La réponse de gts2 m'aurait bien aidé aussi mais je ne sais pas si je serais parvenu à arriver à bout de cette démo avec.
Merci encore à tous, à bientôt.


