Inscription / Connexion Nouveau Sujet
salut
quand on dérive un produit vectoriel ça marche comme la dérivée d'un produit de fonction.
tu vas donc trouver facilement les 2 premiers termes de l'accélération. pour la 3e terme, il faut utiliser la formule de transfert de repère pour les dérivées vectoriels (il y a un nom à cette formule mais je l'ai oublié)
ça doit être ça ^^ ça fait intervenir le vecteur rotation entre R et R' d'où le double produit vectoriel
Enfait je me demande pourquoi [d(O'M)/dt]R = ( R'/R)^(O'M) car en utilisant varigon ça donne [d(O'M)/dt)]R = [d(O'M)/dt)]R' +
R'/R)^(O'M) car en utilisant varigon ça donne [d(O'M)/dt)]R = [d(O'M)/dt)]R' +  R'/R^(O'M) ...
R'/R^(O'M) ...
ça voudrait dire que [d(O'M)/dt)]R' = o ? pourquoi ?
merci

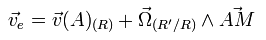
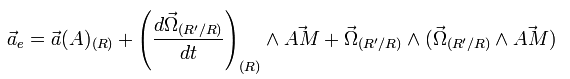
 Merci d'en faire autant la prochaine fois !
Merci d'en faire autant la prochaine fois ! 

