Bonjour à tous,

Cette fois je ne reviens pas pour un exercice en soit (car j'ai déjà effectué les calculs), mais seulement pour la démonstration d'une formule que je n'arrive pas à faire... Je n'ai pas eu de cours sur cette partie, mais même en cherchant sur Internet le cours, je ne comprend pas la logique...

Voici l'énoncé :

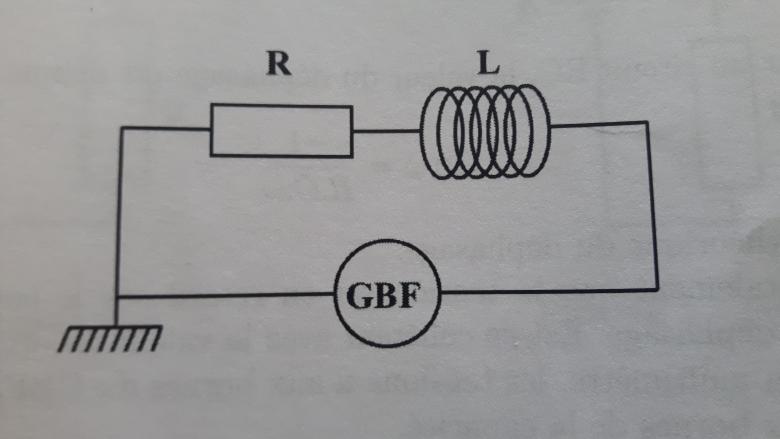
Un circuit RL série est alimenté par une tension sinusoïdale crête à crête de 4V et de fréquence f = 1000 Hz. Prendre une résistance R = 150 (ohm) et la bobine d'inductance L = 40 mH.

Selon le circuit suivant, avec une résistance R = 150 et la bobine d'inductance L = 40 mH (en photo en dessous) :

- En régime alternatif sinusoïdal, la valeur du déphase entre la tension et le courant est imposée par les caractéristiques intrinsèques du circuit : la résistance R, l'inductance L et la pulsation = 2..f. Montrer que, pour ce circuit RL, la valeur du déphasage est définie par :

tan = (L.)/R

Je le rappelle, j'ai déjà fait les calculs, tous ce qu'il me manquent c'est de démontrer la formule. Merci d'avance de votre aide !

AR2