Inscription / Connexion Nouveau Sujet
Accueil l'île de la physique - chimie Forum de physique - chimieListe de tous les forums de physique - chimie SupérieurOn parle exclusivement de physique/chimie, pour le supérieur principalement, les BTS, IUT, prépas... Maths supForum Supérieur de maths sup PhysiqueTopics traitant de Physique [tout]Lister tous les topics de physique - chimie
Niveau maths sup
Partager :

Demande de soutien pour un fil avec un ressort au bout

Posté par
med112 02-01-09 à 22:43

Tout d'abord , j'espère que vous avez tous passez de bonnes vacances d'hiver parce que moi c'était la galère (Oh,non!Je me remets à rimer *_*...).
Sinon , voici un (parmi tant d'autres) problème qui m'énerve un petit peu:
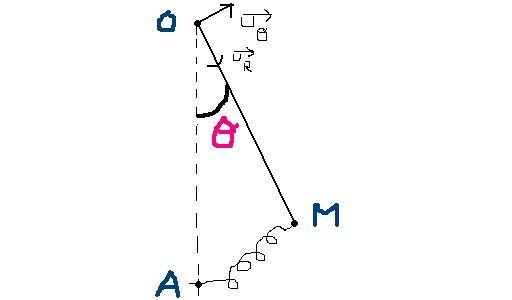
SCHÉMA(en attachement)

On considère le pendule ci-dessous(désolé pour la qualité).
La tige OM de longueur l est de masse négligeable . Le ressort AM de raideur k a une longueur à vide nulle . Le point matériel de masse m est situé en M .
Le référentiel d'étude est considéré comme galiléen . L'étude se fait dans le repère polaire (O,\vec{u_r},\vec{u_(theta)}).

-J'ai dressé le bilan des forces (maintenant il m'obéit au doigt et  l'oeil *_*...)
-J'ai le vecteur \vec{AM}=(l-dcos)\vec{u_r}+ dsin\vec{u_(theta)} -Vous trouvez la même chose ?
-J'ai l'énergie cinétique.
PROBLEME: à partir des travaux élémentaires des différentes forces s'exerçant sur M , établir l'expression de l'énergie potentielle Ep() en fonction de m,g,,k,l et d.Et Ep(0)=0
Il y a d'autres questions après mais j'essaierai de me débrouiller.

Demande de soutien pour un fil avec un ressort au bout

Posté par
donaldosre : Demande de soutien pour un fil avec un ressort au bout 02-01-09 à 23:18

Tu es sûr de la composante \vec{u_{\theta}} de \vec{AM}?

Ce qu'on te demande ensuite c'est de calculer le travail des forces sur un déplacement élémentaire:

\delta W=\sum\vec{F}.\rm{d}\vec{r} (simple dans ce cas particulier)

Ensuite, il suffit de faire le lien entre travail et énergie potentielle pour une force conservative.

Posté par
med112re : Demande de soutien pour un fil avec un ressort au bout 03-01-09 à 10:27

Oui donaldos ,leur travail vaut l'opposé de la dérivée de l'énergie potentielle, pour l'énergie potentielle de pesanteur j'ai : mgl(1-cos).
Mais il me faut du d et je n'arrive pas à le faire apparaître pour l'autre énergie élastique , est-ce que ça pourrait être (k*(AM)^2)/2?
Mais sinon pour AM j'ai fait OM-OA en sachant que OM vaut l\vec{u_r} et OA vaut d(cos\vec{u_r}-sin\vec{u_(theta)}).

Posté par
donaldosre : Demande de soutien pour un fil avec un ressort au bout 03-01-09 à 14:36

A priori, dans cet exercice (et pour ce que je vois de l'énoncé), on te demande de passer par le calcul du travail pour déterminer l'énergie potentielle et non pas d'utiliser les formules connues.

Essaie donc de déterminer l'écriture de chacune des forces s'exerçant sur le point matériel M et effectue ensuite le calcul du travail de ces forces pour un mouvement élémentaire, de la façon la plus classique qui soit. Tu retrouveras alors (ou pas...) des résultats qui te seront familiers.

Posté par
med112re : Demande de soutien pour un fil avec un ressort au bout 03-01-09 à 16:54

La tension du fil ne travaille pas et la force de frottements n'est pas conservative , il me reste alors la pesanteur et l'élasticité du ressort.
\vec{P}=m\vec{g} pour la pesanteur
\vec{T}=-kl\vec{AM}/AM pour le ressort où l est la longueur d'étirement du ressort.
Mais que représente ton d\vec{r} donaldos?
Sinon après je sais pas quoi dire d'autre.

Posté par
donaldosre : Demande de soutien pour un fil avec un ressort au bout 03-01-09 à 19:15

\rm{d}\vec{r} c'est simplement un mouvement élémentaire, une variation du vecteur position \vec{r}:

\vec{r}=r\vec{u_r}

d'où:

\rm{d}\vec{r}=\frac{\rm{d}r}{\rm{d}t} \vec{u_r}+r\frac{\rm{d}\theta}{\rm{d}t}\vec{u_{\theta}

Ce qui se simplifie ici (r=l constant notamment).


Posté par
med112re : Demande de soutien pour un fil avec un ressort au bout 03-01-09 à 20:23

Ce qui nous donne :

W(\vec{P})=m\vec{g}.d\vec{r}
                                    
=mgl\frac{dtheta}{dt}sin
Je sais alors trouvers une primitive.
Mais pour le ressort j'y arrive toujours pas.

Posté par
donaldosre : Demande de soutien pour un fil avec un ressort au bout 03-01-09 à 21:03

C'est pourtant le même principe que pour le poids.

Exprime l'effort exercé par le ressort à partir de \vec{AM}. Tu l'as décomposé selon \vec{u_r} et \vec{u_{\theta}, tu ne devrais donc avoir aucun problème pour calculer le produit scalaire avec \rm{d}\vec{r}.

Posté par
med112re : Demande de soutien pour un fil avec un ressort au bout 03-01-09 à 23:31

Le produit scalaire entre \vec{AM} et d\vec{r} nous donne:
(l-dcos)\frac{dr}{dt} + drsin\frac{d\theta}{dt}
Mais là pour une primitive , c'est pas aussi facile que pour le précédent.

Posté par
donaldosre : Demande de soutien pour un fil avec un ressort au bout 03-01-09 à 23:35

Que peux-tu dire de \frac{\rm{d}r}{\rm{d}t} ici?

Posté par
med112re : Demande de soutien pour un fil avec un ressort au bout 04-01-09 à 13:05

Ici , nous avons r=l qui est constant soit \frac{dr}{dt}=0
Le produit scalaire vaut alors drsin\frac{d\theta}{dt}
Mais après je ne sais plus continuer car je ne sais pas traduire l la longueur d'étirement du ressort et pour AM au dénominateur , est-ce que ça vaut \sqrt{(l-dcos\theta)^2 + (dsin\theta)^2} ?

Posté par
donaldosre : Demande de soutien pour un fil avec un ressort au bout 04-01-09 à 14:15

Sauf erreur de ma part, l'expression de l'effort exercé par le ressort s'exprime simplement par:

\vec{T}=-k\vec{AM}

PS: petite erreur de ma part, l'expression d'un mouvement élémentaire du point matériel, c'est:

\rm{d}\vec{r}=\rm{d}r \vec{u_r}+r\rm{d}\theta\vec{u_{\theta}

Posté par
med112re : Demande de soutien pour un fil avec un ressort au bout 04-01-09 à 17:10

Exact , donc nous avons :
W(\vec{T})=-kdrsind()
Et après je trouve une primitive et j'attaque la suite du dm.Si c'est ça , merci donaldos de m'avoir accordé ton attention.Peut-être que c'était trop trivial pour certain , je l'avoue ,mais au moins on ne voit pas des APPARITIONS de formules de physique.

Posté par
donaldosre : Demande de soutien pour un fil avec un ressort au bout 04-01-09 à 18:03

Ça me semble correct.

Bon courage pour la suite.

PS: je suis aussi partisan du "je n'écris que ce que je comprends".

Posté par
med112re : Demande de soutien pour un fil avec un ressort au bout 08-01-09 à 16:12

P.S:Est-ce qu'il y a conservation de l'énergie mécanique ? Il y a un petit problème avec la force de frottements qui n'est pas conservative.

Posté par
donaldosre : Demande de soutien pour un fil avec un ressort au bout 08-01-09 à 17:45

Je ne me rappelle pas avoir vu de frottements dans ton problème mais s'il y en a, alors non, il n'y a pas conservation de l'énergie mécanique.

Posté par
med112re : Demande de soutien pour un fil avec un ressort au bout 08-01-09 à 18:26

Très bien , thank you donaldos !


Rechercher
Menu
Espace membre
Changer d'île
Mentions légales - Retrouvez cette page sur l'île de la physique - chimie
© digiSchool 2025

Vous devez être membre accéder à ce service...

Pas encore inscrit ?

1 compte par personne, multi-compte interdit !

Ou identifiez-vous :

Rester sur la page

Désolé, votre version d'Internet Explorer est plus que périmée ! Merci de le mettre à jour ou de télécharger Firefox ou Google Chrome pour utiliser le site. Votre ordinateur vous remerciera !