Inscription / Connexion Nouveau Sujet
Déformation d un ressort
Bonjours pourriez vous m aider pour cet exercice s il vous plait ?
Une masse m glisse sans frottement sur un plan incliné d un angle
avec l horizontale ( figure). Elle est lâché du point À situe à une distance d du point O sans vitesse initiale et finit par percuter un ressort ( de raideur k et de longueur à vide l0) fixé en O. Le ressort possède initialement sa longueur à vide.
1-Tracer l'énergie potentielle Ep(x) en fonction de x.
2- A quelle condition la masse atteint elle le point O? Interpréter en terme de barrière de potentiel.
3- Quel est mouvement de la masse s'il n'y a pas collision en O?
4-Que se passe t il , qualitativement , si on prend en compte les frottements ?
1: système : masse m
Référentiel : terrestre supp galiléen
Bilan des forces : le poids P =mg quand x 
l0 et si x 
l0 alors les forces appliquées sont T=-k(l-l0)ux et P= mg
Ensuite je pense qu il faut utilisé la loi de l énergie cinétique et en déduire l énergie potentiel car l énergie mécanique est constante et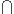 
E =-dEp
Mais je n arrive pas vraiment à exprimer la loi de l énergie cinétique....
Je bloque alors pourriez vous m aider s'il vous plaît?
Salut,
Soit L1 la longueur max parcourue par le mobile (au moment où sa vitesse devient nulle (par la compression du ressort))
Variation d'énergie potentielle du mobile sur ce trajet : M.g.L1.sin(alpha)
Cette énergie aura été "emmagasinée" dans le ressort sous forme d'énergie potentielle élastique.
Or l'énergie potentielle élastique d'un ressort de constante k est Ee = 1/2.k.(Delta L)² avec Delta L la variation de longueur du ressort par rapport à sa longueur hors contrainte (Lo)
Et dans le cas présent : L1 = L - Lo + Delta L
--> m.g.L1.sin(alpha) = 1/2.k.(L1 - L + Lo)²
-----
Pour atteindre le point O, il faudrait que L1 = L soit Lo = Delta L (Ce qui n'est pas possible avec un ressort "classique")
Soit donc : m.g.L.sin(alpha) = 1/2.k.(Lo)²
-----
Si pas de collision en O (et ressort pas à butée mécanique spires contre spires), après la compression du ressort (qui amène le mobile a avoir parcouru la distance L1), le ressort va repousser le mobile vers le haut de la pente et lui communiquer une énergie cinétique juste suffisante (lorsque le ressort est revenu juste à sa longueur Lo) pour le faire remonter la pente juste jusqu'au point A de lacher initial.
Tout ceci, si aucune perte (frottement) n'a lieu.
Et puis le mobile va redescendre .... et le cycle recommence à l'infini.
Tout ceci, si aucune perte (frottement) n'a lieu. (ce qui est évidemment impossible).
-----
Si y a des frottements ...
Plusieurs cas à envisagés :
a) coeff de frottement entre mobile et plan incliné suffisamment grand ---> le mobile ne quitte pas le point A.
b) coeff de frottement entre mobile et plan incliné pas trop grand, la masse descent, va comprimer le ressort (moins fort que si pas de frottement) et le ressort va repousser le mobile vers le haut de la pente ... mais le mobile n'atteindra pas le point A, ensuite il descendra et ...
Le mobile va osciller sur le plan incliné mais avec une oscillation amortie ... jusquà l'arrêt du mobile.
Sauf distraction. 
Annuler
connectez vous