Inscription / Connexion Nouveau Sujet
Décomposition en série de Fourier
Bonjour à tous, je dois tracer sur un graph les fonctions suivantes:
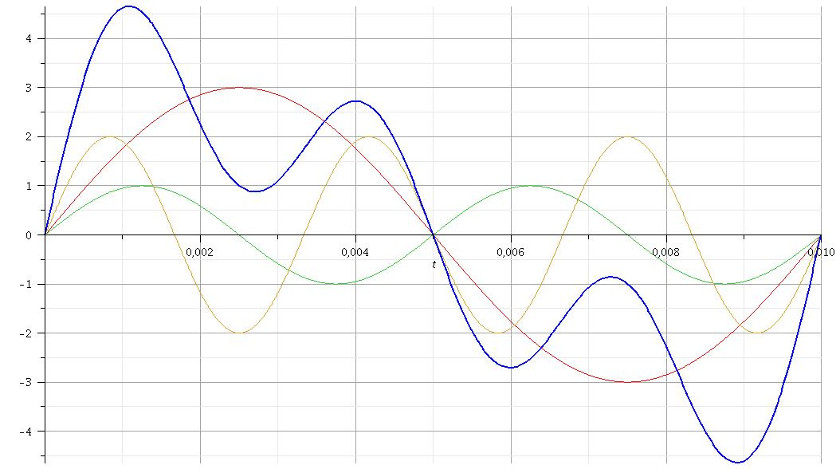
U1(t)=3sin(2π*100t)
U2(t)=sin(2π*200t)
U3(t)=2sin(2π*300t), correspondant à la décompo en série de Fourier de U(t)=3sin(2π*100t) + sin(2π*200t) + 2sin(2π*300t).
Mais je ne sais pas comment m'y prendre car forcément en remplaçant t par 0, 1, 2, ... je retombe sur U(t)=0... Merci!
Bonsoir
Tu traces d'abord la sinusoïde correspondant à U1 en faisant, par exemple, correspondre 12 cm à une période.
Tu traces ensuite dans le même repère la sinusoïde correspondant à U2 en remarquant que sa période est la moitié de la précédente.
Tu traces ensuite la sinusoïde correspondant à U3 en remarquant que sa période est le tiers de celle de U1.
Évidemment, tu peux faire apparaître le résultat final grâce à une calculatrice graphique ou un ordinateur équipé d'un tableur.
Cela devrait ressembler aux courbes ci-dessous...
Une tension sinusoïdale peut s'écrire : u(t)=Um.sin(
.t+
)
la pulsation étant égale à :
Par identification, la phase initiale est toujours nulle.
La fréquence de U1 est f=100Hz ; celle de U2 est 2f, celle de U3 est 3f. Il s'agit bien de superposer le fondamental U1 aux harmoniques U2 et U3. La somme U aura la fréquence du fondamental soit f = 100Hz.
La période étant l'inverse de la fréquence, doubler la fréquence est équivalent à diviser la période par 2...
Tu peux tracer à main levée les trois sinusoïdes correspondant aux tensions U1,U2 et U3 en tenant compte de mes remarques précédentes sur les périodes. Ensuite, tu peux obtenir la somme : tu devrais obtenir la courbe bleue...
Annuler
connectez vous