Inscription / Connexion Nouveau Sujet
Decharge d'un condensateur dans un autre
Bonjour, j'ai un soucis au sujet d'un exercice d’électricité dont voici le schema :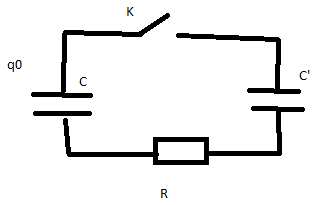
Le condensateur de capacité C est chargé sous une tension U0. Il est branché à l'instant initial sur un autre condensateur de capacité C', initialement dechargé.
Determiner l'évolution des tensions u(t) et u'(t) (c'est à dire des deux condensateurs)
Determiner l'évolution de l'intensité I(t)
Determiner l'energie E1 dissipé par effet joule.
Le problème est que je ne sais pas d'ou partir... J'ai ecris la loi des mailles
U-Ur-U'=0
U-Ri-U'=0
U-C'dU/dt -U'=0?
mais comment je fais à partir de cela pour trouver la suite car je ne peut pas résoudre cette équation différentielle puisque que U varie au cour du temps...
merci
Edit Coll : image placée sur le serveur de l'  Merci d'en faire autant la prochaine fois !
Merci d'en faire autant la prochaine fois ! 
![]()
Bonsoir Mrfrodo42,
ce n'est pas un exercice très difficile ; malheureusement je ne dispose que de mon corrigé manuscrit, et le retaper pour le mettre sur le forum va prendre beaucoup trop de temps. Alors, bien que ce ne soit pas très sympa pour d'autres personnes intéressées, je vais faire ainsi : en cliquant ici ![]() , tu pourras télécharger une archive où j'ai mis mon énoncé et quatre demi-pages de corrigé (attends qqes secondes pour avoir le panneau classique "ouvrir ou télécharger").
, tu pourras télécharger une archive où j'ai mis mon énoncé et quatre demi-pages de corrigé (attends qqes secondes pour avoir le panneau classique "ouvrir ou télécharger").
Tu adapteras toi-même mes notations avec celles de ton propre énoncé.
Je mettrai ultérieurement mon corrigé au propre, afin que d'autres étudiants dans la même situation que toi puissent en profiter.
Bonne lecture.
Bonjour, je vous remercie beaucoup pour votre aide je me doute que ce type d'exercice peut paraitre simple mais comme je n'en ai jamais traité...
je pensais plus qu'il fallait faire une loi des mailles, et arranger l'équation .
merci beaucoup pour votre aide
Je mets les 2 tensions (u et u' avec la flèche vers le haut) :
u - u' - R.i = 0
i = -C.du/dt
i = C'.du'/dt
du/dt - du'/dt - R.di/dt = 0
-i/C - i/C' - R.di/dt = 0
di/dt + i(C+C')/(RCC') = 0
i(t) = K.e^[-(C+C').t/(RCC')]
i(0) = Uo/R --> K = Uo/R
i(t) = (Uo/R).e^[-(C+C').t/(RCC')]
---
du/dt = -i/C
du/dt = -(Uo/(RC)).e^[-(C+C').t/(RCC')]
u(t) = (Uo/(RC)) * RCC'/(C+C') * e^[-(C+C').t/(RCC')] + K1
u(t) = Uo * C'/(C+C') * e^[-(C+C').t/(RCC')] + K1
u(0) = Uo --> Uo * C'/(C+C') + K1 = Uo
K1 = Uo(1 - C'/(C+C')) = Uo.C/(C+C')
u(t) = Uo/(C+C') * [C + C'e^(-(C+C').t/(RCC'))]
---
du'/dt = i/C'
du'/dt = (Uo/(RC)).e^[-(C+C').t/(RCC')]
u'(t) = -(Uo/(RC))*RCC'/(C+C') * e^[-(C+C').t/(RCC')] + K2
u'(t) = -Uo*C'/(C+C') * e^[-(C+C').t/(RCC')] + K2
u'0) = 0 ---> -Uo*C'/(C+C') + K2 = 0
K2 = Uo*C'/(C+C')
u'(t) = Uo*C'/(C+C') * (1 - e^(-(C+C').t/(RCC'))]
---
E1 = S(de0à+oo) R.i² dt
E1 = R (Uo/R)² * S(de0à+oo) e^[-2.(C+C').t/(RCC')] dt
E1 = -Uo²/R * RCC'/(2.(C+C')) * [e^[-2.(C+C').t/(RCC')](de0à+oo)
E1 = Uo²/R * RCC'/(2.(C+C'))
E1 = Uo² * CC'/(2.(C+C'))
... On remarquera que E1 est indépendante de la valeur de R.
-----
Sauf distraction. 
bonjour je vous remercie pour votre aide, j'ai parfaitement compris le principe de l'exercice j'essaie à présent de le refaire.
merci je me sens déjà plus rassuré pour le ds à venir.
désolé du double post(je ne trouve pas la touche pour modifier le message) mais il y a une petite chose que je ne comprend pas mais la suite est tout à fait clair:
pourquoi au début on écrit:
i = -C.du/dt
i = C'.du'/dt
je ne comprend pas l'origine du signe "-" ?
merci beaucoup!
bonjour Mrfrodo42,
c'est parce que le condensateur C se décharge, donc u diminue avec se temps et du/dt est négative ; au contraire C' se charge et du'/dt est positive. Les équations données par JP (et les miennes aussi dans mon manuscrit) sont écrites en travaillant avec un courant i positif. D'où le signe - devant le terme en du/dt.
Il y a une analogie très simple entre cet exercice et une expérience qu'on a tous fait ou vu faire : deux récipients sont reliés par un tuyau mini d'un robinet. L'un est plein, l'autre est vide. Lorsqu'on ouvre le robinet, le récipient plein se vide et l'autre se remplit ; la manipe s'arrête lors que les niveaux dans les deux récipients sont à la même hauteur. Fais l'analogie entre la hauteur d'eau dans chaque récipient et la ddp u et u' aux bornes de chaque condensateur. Si ça peut t'aider à comprendre.
bonjour, et merci pour cet explication!
je pense avoir bien compris maintenant je vous remercie beaucoup pour votre aide !
bon dimanche!
J'ai choisi pour i , u et u' les sens indiqués sur mon dessin.
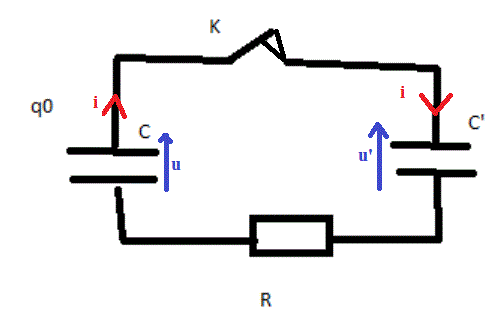
On remarque que :
Pour C', i et u' sont de sens contraires, c'est une convention récepteur qui impose : i = C'.du'/dt
Pour C, i et u sont de mêmes sens, c'est une convention générateur qui impose : i = - C.du/dt

bonjour, désolé de mon temps de réponse mais la semaine je n'ai pas trop acces à internet.
je tenais juste à vous remercier pour votre réponse qui m'a beaucoup aidé ! je me sens en confiance pour le ds de lundi !
Bon j'ai fais le même genre d'exercice(avec C=C' comme seule différence) mais j'ai toujours pas compris pourquoi j'ai des résultats différent avec ma méthode j'ai d'abord écrit :
U+U'+RI=0
en suite comme U=q/C et U'=q'/C, i=dq'/dt avec q+q'=q0(charge totale avant décharge)
on a :
dq'/dt= -dq/dt car q'=q0-q
l'équation donne:
q/C+(q0-q)/C-Rdq/dt=0
on obtient
Rdq/dt=-q0/C
Rdq=-q0/Cdt
R(q-q0) = -q0t/c
q=(Rq0-q0t/c)/R
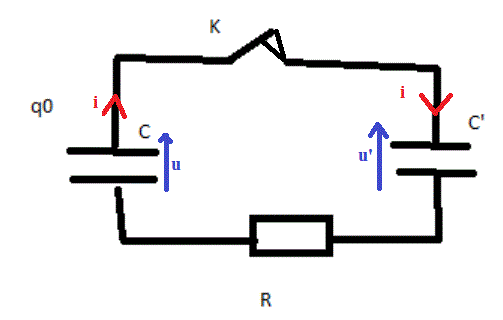
Je m'arrête à ta première relation, soit : U+U'+RI=0
Elle est fausse., il faut commencer par bien comprendre la loi des mailles ... sinon on n'arrivera jamais à rien de bon.
Avec les sens des tensions et courant du dessin, on a : u - u' - R.i = 0
*****
Inutile d'essayer de poursuivre tant que tu n'auras pas compris cela (j'ai écrit : COMPRiS).

Merci de votre réponse, je comprends exactement ce que tu veux dire c'est une erreur de ma part, mais j'ai toujours pas la même chose que vous :
U=U'+RI
en suite comme U=-q/C(convention récepteur) et U'=q'/C, i=dq'/dt avec q+q'=q0(charge totale avant décharge)
on a :
dq'/dt= -dq/dt car q'=q0-q
l'équation donne:
-q/C=(q0-q)/C-Rdq/dt
on obtient
Rdq/dt=-q0/C
Rdq=-q0/Cdt
R(q-q0) = -q0t/C
q=(Rq0-q0t/C)/R
finalement
q=q0(1-t/RC)
Je veux savoir où est mon erreur, ici j'ai le droit ou pas d'utiliser le convention recepteur pour le condensateur vu que ça se comporte comme un générateur?
J'ai fais ainsi car j'ai vu que quand on écrit l'équation de la décharge d'un condensateur sur une résistance R. On utilise la convention recepteur pour la tension au borne du condensateur. Pourquoi cela devrait être différent ici ?
Il est évident que ta réponse finale, soit q=q0(1-t/RC) ne peut être que fausse.
... Il suffit de voir ce que devient q lorsque t --> +oo pour en être persuadé.
j'ai le droit ou pas d'utiliser le convention recepteur pour le condensateur vu que ça se comporte comme un générateur?
On s'en fout, on utilise les conventions qu'on veut ... MAIS, une fois que c'est choisi en début d'exercice (cela se fait avec les sens des tensions et courants qu'on choisi par le sens des flèches sur le schéma) ... on ne pas les modifier en cours de calculs.
Ces notions de récepteur ou générateur ne sont, dans maints cas, pas possible à choisir "intelligemment".
Par exemple (pas le cas ici, mais peu importe), dans un circuit oscillant type RLC; le C et le L se comportent au cours du temps tantôt en générateur, tantôt en récepteur ... tant que l'oscillation persiste.
Sur un schéma, on peut TOUJOURS choisir pour n'importe quel composant une représentation (de U et de I) pour un récepteur ou bien pour un générateur ...
Mais une fois fait, on ne peut plus y changer.
Il faut cependant tenir compte des choix fait sur le schéma pour écrire les équations des mailles et noeuds ... et pour tirer certaines conclusions des résultats obtenus.
------------
Avec les sens de tensions et courant que j'avais choisi (arbitrairement) sur le schéma, on a :
u - u' - R.i = 0
avec :
i = -C.du/dt
i = C'.du'/dt
q/C - q'/C' + RC.du/dt
q/C - q'/C' + R.dq/dt = 0
q + q' = qo
--> q/C - (qo - q)/C' + R.dq/dt = 0
q/C + q/C' + R.dq/dt = qo/C'
dq/dt + q * (C+C')/(RCC') = qo/(RC')
q(t) = qo.C/(C+C') + K.e^(-t*(C+C')/(RCC'))
Q(0) = qo --> qo.C/(C+C') + K = qo et donc K = qo*(1 - C/(C+C')) = qo.C'/(C+C')
q(t) = qo.C/(C+C') + qo.C'/(C+C').e^(-t*(C+C')/(RCC'))
Et si C=C' -->
q(t) = (qo/2) * (1 + e^(-t*(2/(RC)))
-----
Remarque quand même : Comme je l'ai dit, on peut choisir la convention qu'on veut (générateur ou récepteur) pour chacun des composants d'un schéma ...
Cela n'empêche pas (même si on n'est pas obligé) de choisir la convention dont on sait qu'elle est "la meilleure", par exemple, une résistance ne se comportera jamais comme un générateur mais toujours comme un récepteur ... il est donc "plus normal" de choisir sur un schéma une convention récepteur pour une résistance.
Par contre, dans des circuits autres que simplistes, les C et les L peuvent aussi bien se comporter en récepteur que en générateur, pareil d'ailleurs pour les "générateurs", par exemple un accu peut de décharger dans le circuit extérieur (il se comporte donc là en générateur) ... mais il peut aussi se comporter en récepteur (par exemple lors de sa recharge) ...
En résumé :
Sur un schéma on peut choisir la convention qu'on veut pour chacun des composants ...
mais le choix fait, on ne peut plus le modifier.
Et il faut tenir compte des choix faits sur le schéma pour écrire les relations (mailles et noeuds) ... et pour tirer des conclusions judicieuses des résultats.
Sauf distraction.

Bonjour a tous,
Je me permet de relancer l exercice car j ai quasiment le meme a faire.
Je dois aussi retrouver l expression de l'energie dissipee par effet Joule en faisant en bilan energetique.
Malheureusement je ne retrouve pas le meme resultat que JP...
En prenant q(t)=C*u(t) avec u(t)=Uo/(C+C') * [C + C'e^(-(C+C').t/(RCC'))]
et u'(t)=Uo*C'/(C+C') * (1 - e^(-(C+C').t/(RCC')))
Voici mon raisonnement -1/2C*d(q^2)/dt-1/2C'*d(q'^2)/dt=Ri^2 ce qui m amène à  Ec-
Ec- Ec'=Ejoule ce qui donne -q^2(+inf)/2C+q^2(0)/2C-q^2(+inf)/2C'+q'^2(0)/2C'=Ejoule
Ec'=Ejoule ce qui donne -q^2(+inf)/2C+q^2(0)/2C-q^2(+inf)/2C'+q'^2(0)/2C'=Ejoule
mais pas moyen de retomber sur Ejoule=Uo² * CC'/(2.(C+C'))
merci d avance 
Quel mic-mac.
u(t) = Uo/(C+C') * [C + C'e^(-(C+C').t/(RCC'))]
u(t-->oo) = Uo * C/(C+C')
Q(0) = C.U(0)
Q(t-->oo) = (C+C') * Uo * C/(C+C') = C.U(0)
Ce qui correspond bien à une conservation de la charge.
E(0) = (1/2) * C.Uo²
E(t-->+oo) = (1/2).(C+C').(u(t-->oo))² = (1/2).(C+C') * Uo² * C²/(C+C')² = (1/2) * Uo² * C²/(C+C')
Delta E = (1/2) * Uo² * C²/(C+C') - (1/2) * C.Uo²
Delta E = (1/2) * C.Uo² * (C/(C+C') - 1) = (1/2) * C.Uo² * (C - C'-C)/(C+C')
Delta E = - (1/2). C.C'/(C+C') . Uo²
Delta E = - C.C'/(2.(C+C')) . Uo²
Il a donc eu une perte d'énergie égale à [C.C'/(2.(C+C')) . Uo²] ... cette énergie a été dissipée dans la résistance... ce qui peut se vérifier en calculant cette énergie autrement, par :
S(de0 à +oo) R.i² dt avec i(t) = (Uo/R).e^[-(C+C').t/(RCC')] ... qui donne le même résultat.
Sauf distraction. 


