Inscription / Connexion Nouveau Sujet
De léquation différentielle à l'équation de récurrence
Bonjour,
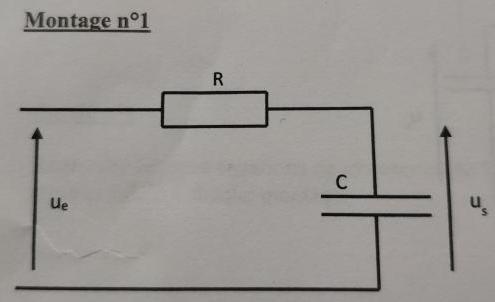
voici mon problème pour un DM je dois "Déterminer l'équation différentielle vérifiée par la tension de sortie us(t)" de plusieurs montages. Le sujet nous donnant les valeurs suivantes :
R = 1.0 kOhm
L = 1.0 H
C = 1.0 uF
Te = 1.0 us (période d'échantillonnage)
et nous rappelle que:
Ur = r*i
UL = L*(di/dt)
i = C*(dUC/dt)
alors je sais déjà que ici dt c'est Te (enfin il me semble)
il m'est aussi préciser que ue(t) = Xn en numérique et us(t) = Yn en numérique.
alors cela peut paraître simple sauf que voilà je suis incapable de trouver ces équations différentielles et cela fait déjà plus d'une heure que je planche sur le premier montage... alors si une personne pourrait m'aider ou me guider sur le bon chemin cela m'aiderai beaucoup s'il vous plait.
Bonjour
alors je sais déjà que ici dt c'est Te (enfin il me semble)
(di/dt) représente la dérivée de i(t) par rapport à t.
(dUc/dt) représente la dérivée de Uc(t) par rapport à t.
Sinon, il suffit d'appliquer la loi d'addition des tensions en utilisant les formules fournies.
Si les deux notions que j'ai évoquées dans mon premier message ne te sont pas familières (notion de dérivée par rapport au temps, additivité des tensions dans un circuit série) ne te sont pas familières, je ne vois vraiment pas comment tu vas pouvoir t'en sortir... Tu as tout de même suivi un cours sur tout cela... Commence par l'étudier attentivement .
Bah ouai j'ai bien eu un cours sauf que bémol j'ai rien capté au cours peut tu (si possible) me donner un début de réponse (pas la réponse à l'exercice mais un exemple de réponse possible) s'il te plait ?
Alors attend, voici ce que j'ai trouvé dit moi si je suis sur la bonne piste s'il te plait.
Ue(t) = Ri(t) + Us(t) avec q(t) la charge du condensateur.
donc on as Us(t) = (q(t)/C) et i(t) = (dq(t)/Te) = C*(du(t)/Te)
donc l'équation différentielle ici serait :
Ue(t) = RC*(du(t)/Te) + Us(t)
(RC peut il se remplacer par Tau ici ? et Te est il à la bonne place ? ou faut il laisser dt ?)
Pas tout à fait.
OK pour la première équation mais ensuite, je ne vois pas ce que Te (grandeur non définie dans tes messages) vient faire ici.
En régime variable, la charge q dépend de la date t. On peut donc définir une fonction f telle que :
l'intensité instantanée représente la dérivée de q(t) par rapport à t. Les mathématiciens noteraient :
RC a la dimension d'une durée ; on l'appelle effectivement “constante de temps” ici.
Donc du coup cela donnerai quelque chose comme :
Ue(t) = RC * (du(t)/dt) + Us(t) ? mais du coup c'est sa l'équa diff ?
Tu as juste oublié un indice :
Cette équation établit une relation entre la variable inconnue us(t) et la dérivée par rapport au temps de cette inconnue, sachant que la tension d'entrée ue(t) est en général donnée par l'énoncé. Il s'agit bien d'une équation différentielle du premier ordre.


