Inscription / Connexion Nouveau Sujet
Cylindre chargé et électrostatique.
Bonjour,j'aurai vraiment besoin d'aide pour cet exo car il a de forte chance de tombé dans un de mes devoir.
J'ai essayé de faire les question 1,2,4,mais c'est assez dur pout moi.
L'énoncé et le schéma sont en bas.
Et voici ce que j'ai pu écrire pour l'instant:
***Solution manuscrite supprimée***
***Enoncé scanné supprimé***
Bonjour,
OK pour tes expressions du vecteur champ E dans les trois cas à une erreur près : pour r>R3, h doit disparaître de l'expression. Pour l'énergie, tu dois savoir que celle-ci se calcule comme si elle était localisée dans tout le domaine d'existence du champ avec la densité volumique
Tu as donc une somme de deux intégrales à calculer :
celle de l'énergie localisée entre R2 et R3
+
celle localisée entre R3 et l'infini.
C'est là que les choses se compliquent car tu vas tomber sur une valeur infinie : logique : tu as calculé le vecteur champ créé par le cylindre en considérant celui-ci comme infiniment long !
Pour calculer l'énergie du tronçon de longueur L, il faudrait être capable de déterminer le vecteur champ créé par ce tronçon de longueur L et cela : je doute que ce soit à ton programme...
Cet exercice a été donné par ton professeur ou tu l'as trouvé sur internet ?
Suggestion :
Si tu veux t'entraîner à ce genre d'exercice, remplace "cylindre creux" par "boule creuse" de rayon intérieur R2, de rayon extérieur R3. Cette fois-ci, ta source de champ sera d'extension finie, tu pourras calculer l'expression exacte du vecteur champ créé et tu n'auras pas de problème pour calculer l'énergie.
Bonjour,
Cet exercice a été donné par ton professeur ou tu l'as trouvé sur internet ?
Bonjour vanoise je vais posté plus tard mes nouveaux calculs en utilisant ce que tu m'as dis.
Et bien ça fait partie d'une série d'exo qu'il nous a donner,mais celui là n'a pas été corrigé.
La question 1 et 2),ça va,la 4 c'est différent,même la 3 aussi...
Suggestion :
Si tu veux t'entraîner à ce genre d'exercice, remplace "cylindre creux" par "boule creuse"
Ok je prendrais note,merci

Suivant ce que tu m'as dis vanoise, j'ai We=énergie électrostatique=



 0
0
+ 

Et vaut: r.dr.d
 .dz.
.dz.
J'ai mis 3 intégrale parce mon prof en met 3 pour cette formule (We).
Ton calcul intégral me semble correct ; après intégration de  =0 à
=0 à
 =2
=2 puis de z = 0 à z = L, la seconde intégrale se réduit à :
puis de z = 0 à z = L, la seconde intégrale se réduit à :
ce qui conduit très logiquement à une énergie infinie comme déjà expliqué...
Je ne sais pas si ton professeur a pris le temps de réfléchir à cet exercice avant de le proposer aux étudiants. Je serais curieux d'avoir son corrigé... Mais cela a du bon : cet exercice te pousse à réfléchir et à approfondir tes connaissances !
Je ne sais pas non plus si il a pris le temps d'y penser...
Je vais demander à des amis si ils ont son corrigé,je ne me souviens pas qu'on l'ai corrigé d'ailleurs.
Oui c'est important approfondir ses connaissances et d'augmenter ses notes par la même occasion ^^.
Merci encore pour ton aide vanoise  ,je te poserai peut-être des question pour la question 3) un autre jour j'pense.
,je te poserai peut-être des question pour la question 3) un autre jour j'pense.
La modération veut que je tape tout ça,je comprends,c'est la règle mais c'est super long a taper...
Un conseil si tu as un contrôle bientôt sur ce genre de sujet : pense à ce que j'ai écris le 11-01-16 à 17:56 ; cet exercice est un grand classique et ne pose pas de grosses difficultés puisque la source est d'extension finie.
Merci pour ton conseil vanoise 
Sinon j'ai essayer de faire la question 3)ou l'on me demande de donner l'allure de E en fonction de la variable pertinente.
Voici l'allure que j'ai trouvé(ya deux trait à la fin un au crayon,un au stylo,je sais pas lequel choisir).
Je sais seulement que de 0 à R2 on a une fonction y=0,puis le reste c'est des fonctions inverses.
Mais est-ce bon?
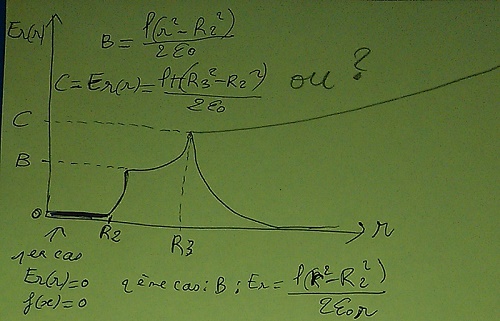
Bonsoir,
Je crois que tes expressions de E sont correctes. En revanche, ta courbe me parait bizarre. Voici ce que j'obtiens sous Maple (unités arbitraires)avec R2 = 1 et R3=1,5R2
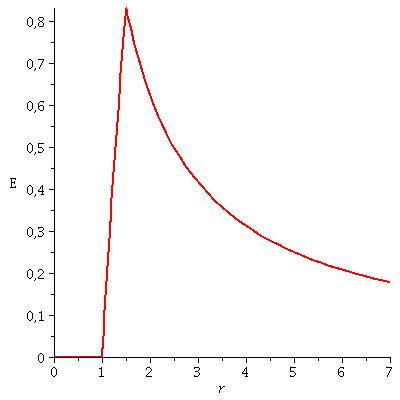


 remercier la personne
remercier la personne
