Inscription / Connexion Nouveau Sujet
Cylindre chargé 2
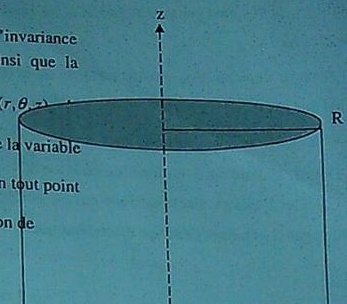
1)Trouver la direction du champs E et la variable pertinente.
2)Calculer la valeur de E en tout point M(

 z) de l'espace.
z) de l'espace.
3)Allure de E en fonction de la variable pertinente.
4)Donner la densité d'énergie électromagnétique en tout point M de l'espace.
5)calculer l'énergie électrostatique pour une portion de cylindre de hauteur h h très grand devant R.
Le schéma est en bas
Et voici ce que j'ai pu dire :
1)E(M)(vecteur)=Er(r).er(vect er).
2)Il y a 2 cas de figure:
r<R et r>R.
Pour le premier cas Er(r)=
 .r/(2
.r/(2 0).
0).
Pour le second cas r>R
Ensuite pour la question 4),j'ai trouvé cela:
We=énergie électromagnétique=
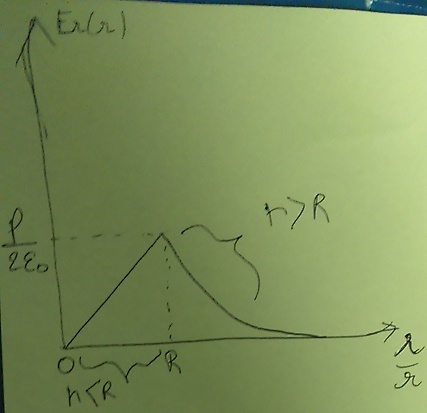
Puis ce que j'ai trouver pour le 3) c'est sur ce graphique:
Bonjour,
D'accord avec toi en ce qui concerne les deux expressions de E
Concernant l'énergie, tu as le même problème que celui déjà expliqué : cette énergie se calcule comme si elle était localisée dans tout le volume d'existence du champ.
A l'expression que tu as obtenue, il faut ajouter celle localisée dans le vide autour du cylindre : le calcul va te conduire à une valeur infinie : je t'ai déjà expliqué pourquoi !
Up
Euh ma réponse 4) n'est pas bonne,n'en tenez pas compte,cependant si on peut m'aider pour le 5...ça serai cool.
Bonjour,
A l'expression que tu as obtenue, il faut ajouter celle localisée dans le vide autour du cylindre : le calcul va te conduire à une valeur infinie : je t'ai déjà expliqué pourquoi !
Ah oui dsl vanoise j'avais oublié donc c'est We=
=
Je trouve une piste pour le 5),mais pourquoi le 3) n'est pas bon?
On a une fonction affine au début,puis une fonction inverse non?


