Inscription / Connexion Nouveau Sujet
Cycle de Stirling inversé
Bonjour,
J'ai une question concernant le rendement pour l'exercice suivant.
On va se servir d'un moteur Stirling pour répondre aux besoins en chauffage en inversant son sens de fonctionnement. Le fluide caloporteur circulant dans le moteur est toujours de l'air assimilé à un gaz parfait diatomique. L'air subira cette fois-ci les transformations réversibles suivantes :
Echauffement isochore de l'état (T1 = 268,1 K , p1 = 1 bar) à l'état (T2 = 293,15 K , p2).
Compression isotherme de l'état (T2 , p2) à l'état (T3 , p3 = 5 bar).
Refroidissement isochore de l'état (T3 , p3) à l'état (T4 , p4).
Détente isotherme de l'état (T4 , p4) à l'état (T1 , p1).
Pour le calcul du rendement, j'ai un COP supérieur à un cycle de Carnot en utilisant les formules :
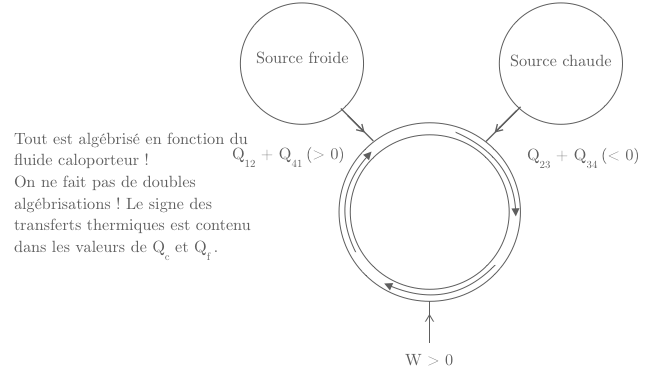
Aussi j'ai fait le diagramme joint, en faisant apparaître le cycle caloporteur.
Merci d'avance si quelqu'un comprend pourquoi j'ai faux !
Bonjour
fiche sur le deuxième principe sur ce forum étudie le cycle de Starling. Tu pourrais la consulter dans un premier temps.
Je crois avoir compris.
La chaleur Q(41) est stockée puis redonnée au fluide caloporteur, donc elle n'est pas comptabilisée en tant que chaleur cédée au milieu extérieur (Sources chaude et froide). Alors il suffit que je mette Q(23) sur mon schéma pour qu'il soit correct ou est-ce que vous pensez que le schéma est faux ?
Tu as compris l'essentiel je crois.
Le transfert de chaleur utile ici correspond uniquement à l'étape 2-3. Le facteur de performance s'écrit donc :
Les étapes 1-2 et 3-4 sont des étapes au cours desquelles le gaz est déplacé de manière isochore d'une source à l'autre. Les échanges de chaleurs lors de ces deux étapes ne sont pas à prendre en compte, que le cycle soit moteur ou récepteur. Cela correspond à ce que tu expliques dans ton dernier message.
Puisque T2=T3=Tc et T4=T1=Tf et puisque le gaz est assimilé à un gaz parfait, il est facile de montrer (première loi de Joule) : . Le cycle de Stirling étudié ici est donc assimilable à un cycle ditherme réversible qui vérifie donc le deuxième théorème de Carnot. Pour le schéma, tu peux n'y pas faire figurer Q34 et Q12. Autre solution : faire figurer un autre bloc appelé « récupérateur » qui recevrait du moteur la chaleur Q12 pour restituer cette quantité lors de l'étape 3-4.



