Inscription / Connexion Nouveau Sujet
Cristallographie
Bonsoir,
dans mon cours de cristallographie j'ai pas compris cette relation dhkl=a/ (h2+k2+l2) qui exprime la distance interréticulaire Pour un réseau cubique,mais la distance interréticulaire entre quels plans interréticulaire?, et comment faire pour démontrer cette relation?
(h2+k2+l2) qui exprime la distance interréticulaire Pour un réseau cubique,mais la distance interréticulaire entre quels plans interréticulaire?, et comment faire pour démontrer cette relation?
j'espère que vous m'apporter quelque élément de réponse.
Merci d'avance.
Bonjour,
Questions surprenantes si tu as un cours de cristallographie sous la main...
Cette distance interréticulaire valable pour le réseau cubique est bien évidemment celle des plans (h k l)
Démonstration : distance de l'origine au plan d'équation
hx + ky + lz = a

salut,merci pour ta réponse !
j'ai pas compris comment faire pour démontrer la relation avec hx + ky + lz = a , sinon cette relation est fausse.
désolé Monsieur,mais si tu peut m'expliquer comment procéder pour la démontrer,car j'ai pas la compris.
Je ne vais pas te faire un cours de cristallographie.
Mais voilà une simple "explication" en deux dimensions. À toi de généraliser à trois dimensions.
Soit un réseau bidimensionnel dont la maille est primitive et carrée.
J'adopte comme unité de longueur sur les axes le paramètre a de la maille.
Je m'intéresse à la famille de droites réticulaires dont un membre passe par les nœuds (2 , 0) et (0 , 3).
Je cherche la distance interréticulaire de ces droites.
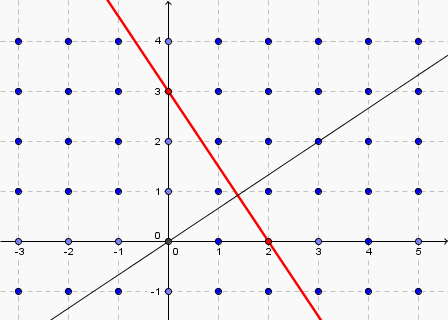
L'équation de la droite rouge est :
ou encore
6 est le ppcm des nombres 2 et 3 qui sont premiers entre eux.
Les indices de Miller de cette famille de droites sont donc (3 2)
Les indices de direction d'une normale à cette famille sont [3 2] (voir la droite en noir sur la figure).
Toute droite d'équation
avec n = 6.m avec m 
 est membre de la famille.
est membre de la famille.
Existe-t-il une droite réticulaire d'équation
La réponse est oui (théorème de Blachet-Bézout). Une solution sera par exemple x = 1 et y = -1 (voir le nœud en vert)
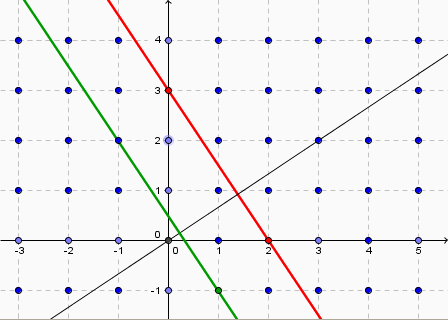
En conséquence l'équation des droites de la famille est
avec n


La droite réticulaire la plus proche de l'origine (et ne passant pas par cette origine...) est en conséquence :
Le point d'intersection de la normale passant par l'origine à cette droite (droite verte) a pour coordonnées :
(programme du lycée...)
Et en conséquence la distance interréticulaire de cette famille de droites est :
Rappel : j'ai pris la longueur a comme unité...
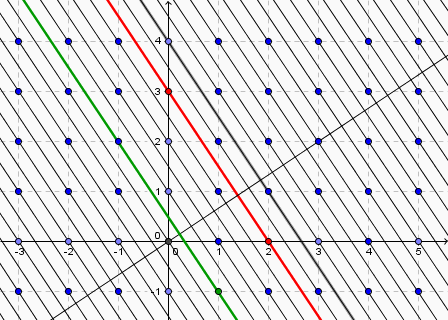
L'extension à trois dimensions est immédiate.
Et donc la distance interréticulaire des plans (h k l) dans un réseau tridimensionnel dont la maille cubique primitive a pour paramètre a vaut :



