Inscription / Connexion Nouveau Sujet
Accueil l'île de la physique - chimie Forum de physique - chimieListe de tous les forums de physique - chimie SupérieurOn parle exclusivement de physique/chimie, pour le supérieur principalement, les BTS, IUT, prépas... Maths supForum Supérieur de maths sup PhysiqueTopics traitant de Physique [tout]Lister tous les topics de physique - chimie
Niveau maths sup
Partager :

Court circuit

Posté par
LalaPTSI 12-01-18 à 20:06

Bonjour,

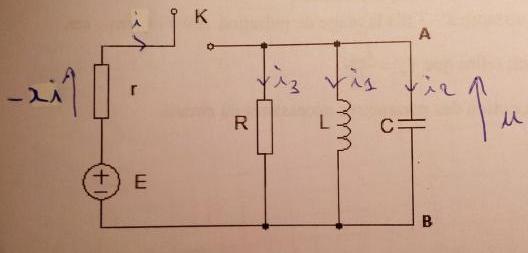
Dans le circuit RLC ci-dessous, on nous dit que le condensateur est initialement déchargé et les courants sont nuls avant la fermeture de l'interrupteur K à t=0.

Seulement j'ai du mal à comprendre car en étudiant le circuit en classe nous avons dit que le condensateur étant déchargé, il est en court circuit à t=0.
Puis à t, c'est la bobine qui est en court circuit.

Pourriez-vous m'expliquer pourquoi ils sont en court circuit ? Comment le sait-on ? Et même, qu'est-ce exactement qu'un court circuit ?...

Merci d'avance !

Court circuit

Posté par
vanoisere : Court circuit 12-01-18 à 20:44

Bonsoir
Il faut savoir qu'en régime permanent toutes les intensités, toutes les tensions, sont indépendantes du temps : leurs dérivées par rapport au temps sont donc nulles en régime permanent.
Cas d'un condensateur : si l'orientation est bien choisi, l'intensité du courant dans la branche du condensateur a pour expression générale ic=C.(duc/dt).
En régime permanent : ic=0 : le condensateur se comporte effectivement comme un interrupteur ouvert. Attention : uc est une constante pas nécessairement nulle.
Cas d'une bobine d'inductance L, de résistance négligeable ; si l'orientation est bien choisie : uL=L.(diL/dt). En régime permanent : uL=0 alors que iL est une constante pas nécessairement nulle. La bobine en régime permanent se comporte bien en interrupteur fermé.
Sinon, tu dois savoir qu'une bobine impose la continuité de l'intensité dans sa branche alors qu'un condensateur impose la continuité de la tension à ses bornes.

Posté par
vanoisere : Court circuit 12-01-18 à 21:01

Petite indication pour la question 3 lorsque K est fermé : appliquer la loi des noeuds :

i=i_{1}+i_{2}+i_{3}
avec :

i=\frac{E-u}{r}\quad;\quad i_{3}=\frac{u}{R}\quad;\quad i_{1}=\frac{1}{L}\int u.dt\quad;\quad i_{2}=C.\frac{du}{dt}
En reportant dans l'expression de la loi des nœuds et en dérivant toutes les variables par rapport au temps pour faire disparaître la primitive, tu obtiens l'équation différentielle vérifiée par u et puisque u=R.i3...

Je te laisse réfléchir à tout cela et continuer.

Tu pourras aussi trouver de l'aide sur cette fiche mais attention : ce que ton énoncé appelle est notée sur la fiche ξ et a une signification différente.

Posté par
LalaPTSIre : Court circuit 12-01-18 à 21:27

Merci pour vos explications !

Donc tout ce que vous m'avez dit dans votre premier message n'est valable qu'en régime permanent donc quand t c'est bien cela ?

Comment puis-je alors savoir qu'en régime transitoire le condensateur est en court circuit ? quel est le rapport avec le fait qu'il soit chargé ou pas ?



Pour la question 3 je bloque justement... J'ai essayé de le faire avec une camarade mais nous n'avons pas compris la correction du prof...

On a effectivement utilisé la loi des noeuds qu'on a dérivé pour obtenir
\frac{di3}{dt}=\frac{di}{dt}-\frac{di1}{dt}-\frac{di2}{dt}

alors j'arrive à remplacer \frac{di1}{dt} et \frac{di2}{dt} par respectivement \frac{u}{L}= \frac{R}{L}i3    et    \frac{d²q}{dt²}=\frac{d²Cu}{dt}=RC\frac{d²i3}{dt²}

En revanche je ne sais pas comment remplacer \frac{di}{dt} car dans la correction on obtient -\frac{i}{r} \frac{du}{dt} et je ne vois pas comment on y arrive... Où est passé le E ?...  Pourquoi le i est sorti de la dérivée ?... j'y ai réfléchi une demi-heure tout à l'heure avec des amis...

Posté par
vanoisere : Court circuit 12-01-18 à 22:17

Je reconnais que les choses ne sont pas très simples. Tu as plusieurs situations différentes à considérer :
1° : La situation t<0 : l'énoncé est claire : K est ouvert et : u=0 et i1=i2=i3 = 0
2° : la situation t=0+ : c'est la qu'interviennent les remarques sur la continuité de u et celle de i1. A cette date t=0+ :
i1=0 ; u=0 :;loi d'Ohm i3=0 ; i=(E-u)/r=E/r ; loi des noeuds dans ce cas particulier : i1=E/r.
3° : le régime transitoire. La méthode que je t'ai indiquée conduit à :

\frac{E}{r}=u\left(\frac{1}{r}+\frac{1}{R}\right)+\frac{1}{L}\int u.dt+C.\frac{du}{dt}
En dérivant par rapport au temps pour faire disparaître la primitive puis en posant u=Ri3 :

0=\frac{R}{L}.u+\left(\frac{R}{r}+1\right)\frac{du}{dt}+RC\frac{d^{2}u}{dt^{2}}
Je te laisse ordonner et simplifier puis identifier les différents termes.
Procéder ainsi me semble un peu plus simple que ton corrigé.
4° : situation t avec K fermé. Cela permet d'obtenir les limites du régime précédent. C'est là qu'intervient le fait que le condensateur se comporte comme un interrupteur ouvert et la bobine comme un interrupteur fermé...
Cela va te permettre d'obtenir les limites asymptotiques de u et des intensités.
Je te laisse réfléchir à tout cela ...

Posté par
LalaPTSIre : Court circuit 12-01-18 à 22:23

D'accord merci beaucoup ! Je comprends un peu mieux ! Je vais laisser tout ça décanter et revenir dessus ! Merci beaucoup !

Posté par
vanoisere : Court circuit 12-01-18 à 22:37

OK ! Pas facile de revenir à l'électricité en CPGE sans en avoir fait au lycée !

Posté par
vanoisere : Court circuit 13-01-18 à 05:58

Je reviens sur ton corrigé que tu ne comprends pas bien. Reprends mon message   12-01-18 à 21:01. Ce qui n'est pas compris en général est la loi d'Ohm appliquée à r :
i=\frac{E-u}{r}\quad
Sinon reprends les deux lignes que j'ai écrites dans ce même message :
i=i_{1}+i_{2}+i_{3}
avec :

i=\frac{E-u}{r}\quad;\quad i_{3}=\frac{u}{R}\quad;\quad i_{1}=\frac{1}{L}\int u.dt\quad;\quad i_{2}=C.\frac{du}{dt}
Dérive chacune par rapport au temps :

\frac{di}{dt}=\frac{di_{1}}{dt}+\frac{di_{2}}{dt}+\frac{di_{3}}{dt}

\frac{di}{dt}=-\frac{1}{r}\frac{du}{dt}\quad;\quad\frac{di_{3}}{dt}=\frac{1}{R}\frac{du}{dt}\quad;\quad\frac{di_{1}}{dt}=\frac{1}{L}.u\quad;\quad\frac{di_{2}}{dt}=C.\frac{d^{2}u}{dt^{2}}

Sachant que u=Ri3, il est possible d'exprimer chaque dérivée de u par une dérivée concernant i3 :

\frac{di}{dt}=-\frac{R}{r}\frac{di_{3}}{dt}\quad;\quad\frac{di_{1}}{dt}=\frac{R}{L}.i_{3}\quad;\quad\frac{di_{2}}{dt}=RC.\frac{d^{2}i_{3}}{dt^{2}}

En reportant dans l'expression dérivée de la loi des nœuds :

-\frac{R}{r}\frac{di_{3}}{dt}=\frac{R}{L}.i_{3}+RC.\frac{d^{2}i_{3}}{dt^{2}}+\frac{di_{3}}{dt}

En ordonnant, on retombe sur le résultat obtenu dans mon message précédent. Ce n'est pas plus simple que la méthode que je t'avais d'abord indiquée. La dérivation par rapport au temps intervient simplement plus tôt dans cette méthode.
\\ 0=\frac{R}{L}.i_{3}+\left(\frac{R}{r}+1\right)\frac{di_{3}}{dt}+RC\frac{d^{2}i_{3}}{dt^{2}}
La suite est facile...

Posté par
gbm Webmasterre : Court circuit 13-01-18 à 12:08

Bonjour à tous,

Encore un circuit RLC parallèle ?!

Décidément, cet exercice te poursuit vanoise en ce début d'année

Bonne continuation et bonne journée,

Posté par
vanoisere : Court circuit 13-01-18 à 16:09

Bonjour gbm
Question de saison ! Pas de problème avec lalaPTSI  mais depuis peu je regarde plutôt deux fois qu'une le pseudo avant d'intervenir !
Bon week-end !

Posté par
LalaPTSIre : Court circuit 13-01-18 à 19:56

Merci beaucoup j'ai compris comment on obtient l'equa diff ! ^^ je crois que j'avais mal recopié le corrigé donc forcément ça n'aide pas beaucoup...

Merci beaucoup en tout cas, j'ai mieux compris et comme j'ai partiel cette semaine (oui des partiels en prépa, quelle idée bizarre :'( ) ça ne sera pas de trop !...


Rechercher
Menu
Espace membre
Changer d'île
Mentions légales - Retrouvez cette page sur l'île de la physique - chimie
© digiSchool 2024

Vous devez être membre accéder à ce service...

Pas encore inscrit ?

1 compte par personne, multi-compte interdit !

Ou identifiez-vous :

Rester sur la page

Désolé, votre version d'Internet Explorer est plus que périmée ! Merci de le mettre à jour ou de télécharger Firefox ou Google Chrome pour utiliser le site. Votre ordinateur vous remerciera !