Inscription / Connexion Nouveau Sujet
Couplage parfait-induction
Salut tout le monde,
J'ai une question s'il vous plait sur la notion du couplage parfait :
"Une pince ampèremétrique est un appareil dont l'extrémité possède la forme d'un tore. En disposant ce tore autour d'un conducteur parcouru par un certain courant le dispositif équipant la pince permet d'en mesurer l'intensité.
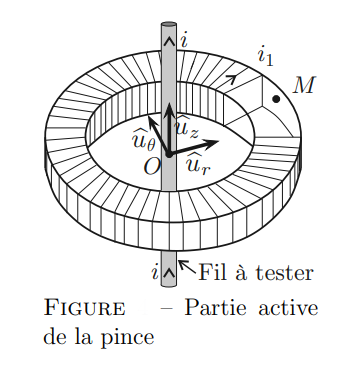
Le dispositif de mesure de la pince ampèremétrique est formé d'un bobinage torique comportant N spires enroulées sur un tore de section rectangulaire de rayon intérieur a, de rayon extérieur b, d'épaisseur c, d?axe (O,z). Le fil conducteur utilisé pour le bobinage possède une résistance linéique  .
.
Un fil rectiligne infini de même axe (O,z) est parcouru par un courant
d'intensité i(t). On note i1(t) l'intensité du courant circulant dans la bobine torique. On se place dans l'approximation des états quasi--stationnaires. "
On a calculé le flux de B crée par le fil et le tore à travers le tore, pour déduire finallement les coefficients d?autoinductance L du bobinage et de mutuelle inductance M entre le fil et le bobinage.
Après j'ai trouvé la phrase suivante dans la correction :
"On remarque que ce qui traduit le couplage parfait entre les circuits primaire et secondaire"
Normalement pour montrer que le couplage est parfait, il faut calculer k= avec Ltore, Lfil les autoinductance du tore et le fil, et montrer que k=1 !
Or j'ai pas pu calculer Lfil : le fil est linéique, donc on peut pas calculer le flux de B à travers le fil, et donc on peut pas trouver Lfil (flux de B à travers le fil =Lfil×i)
Pour récapituler, voila ce que je n'ai pas compris :
1)
"On remarque que
2) Comment peut-on calculer Lfil, sachant que le fil est linéique ?
Merci infiniment pour vos efforts
***Coquille
Je pense que dans ce contexte, ton correcteur à assimilé le fil rectiligne à une spire circulaire de rayon infini, d'où le 1 qu'il fait figurer. Franchement : on peut se passer de cette remarque...
En revanche, tu pose une question intéressante sur l'inductance d'un fil rectiligne de longueur infinie. Une telle inductance est évidemment infinie . En revanche, tu peux calculer l'inductance d'une portion de longueur l d'un fil rectiligne de longueur infinie parcouru par un courant d'intensité i. La méthode consiste à déterminer l'énergie magnétique dans l'espace environnant le fil sur une hauteur l sachant que la densité volumique d'énergie magnétique est B2/(2µo). En écrivant que cette énergie est aussi on obtient le résultat. Résultat sans intérêt pour l'étude d'une pince ampèremétrique...
Merci beaucoup pour votre réponse monsieur vanoise
Quel est le volume a considérer dans ce cas ? (un cylindre de quel rayon ?)
sachant que la densité volumique d'énergie magnétique est B2/(2µo).
En notant ro le rayon du fil :
si
et
si
Comme volume élémentaire, tu peux choisir celui compris entre deux cylindres de rayon r et r+dr, de hauteur commune l :
Énergie magnétique emmagasinée dans la portion d'espace compris entre un plan perpendiculaire au fil de cote z et un plan parallèle de cote (z+l) :
Cela conduit à L infinie. Sans grand intérêt. Retiens tout de même la méthode : elle te sera utile pour l'étude des câbles coaxiaux.
ce qui traduit le couplage parfait entre les circuits primaire et secondaire
Parler de couplage et d'inductance mutuelle suppose une réciprocité de comportement des deux circuits : le circuit n° 1 crée un champ magnétique au niveau du circuit n° 2 et le circuit n° 2 crée un champ magnétique au niveau du circuit n° 1.
Ici, le fil créé un champ magnétique en tout point de la bobine mais que vaut le champ magnétique créé par la bobine torique à l'extérieur de celle-ci ?
Cette remarque suffit à discréditer la phrase de ton corrigé...


