Niveau licence

Couplage de ressort

Posté par
alicia062 11-02-14 à 16:51

Bonjour

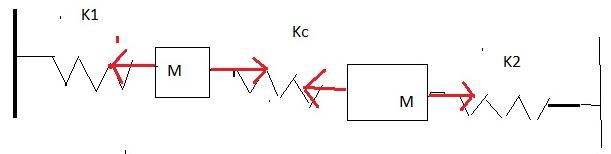
Voici le schéma ci dessous (désolé pour la précision).
-On considère qu'il n'y a pas de frottement
-Et x1 et x2 sont les écarts des positions des masses par rapport à leur position d'équilibre .
(axe x orienté vers la droite)

J'ai deux petites questions concernant l'établissement de l'équation du mouvement des deux masses à partir de la deuxième loi de Newton .

Les équations sont les suivantes :

m1*x1"=-k1x1+kc(x2-x1) idem avec m2 (et -kC)

-Déjà je voudrais savoir vu que ca n'intervient pas dans l'équation, si le poids et la réaction du support se compensent (et donc se serait pour cette raison que les masses se déplacent selon x et pas selon y ) ?
-Ensuite je voulais savoir si dans mon schéma ai je bien représenté les forces de rappel des 3 ressorts (en rouge ) ?

Couplage de ressort

Posté par re : Couplage de ressort 14-02-14 à 15:41

Salut,

Oui c'est ça, tu poses tes équations par rapport à $\vec{x}$ :

D'après le principe fondamental de la dynamique :

$m \times \ddot{x_1} = \vec{F}_{k_1 \rightarrow M} . \vec{x} + \vec{F}_{k_c \rightarrow M} . \vec{x}$

$m \times \ddot{x_2} = \vec{F}_{k_c \rightarrow M} . \vec{x} + \vec{F}_{k_2 \rightarrow M} . \vec{x}$

ce qui équivaut à écrire

$m \times \ddot{x_1} = -k_1 \times x_1 + k_c \times (x_2 - x_1)$

$m \times \ddot{x_2} = -k_c \times (x_2 - x_1) - k_2 \times x_2$

Attention aux sens de tes efforts (qui sont fonction des deux déplacements, qui eux sont dirigés à DROITE de la positions d'équilibre).

Posté par re : Couplage de ressort 15-02-14 à 13:10

Merci d'avoir pris le temps de répondre

Je ne comprend pas votre dernière phrase. Ai je mal représenté les forces ?

Posté par re : Couplage de ressort 15-02-14 à 19:06

Si tu exerces un déplacement x2 vers la droite, le ressort k2 se comprime, dont la force de rappel exercée par ce ressort sur la masse est dans l'autre sens

Posté par re : Couplage de ressort 16-02-14 à 13:53

Et donc ce serait pareil pour la force de rappel du ressort kC et la première masse , elle est dans l'autre sens aussi ?

Posté par re : Couplage de ressort 16-02-14 à 21:52

non ça c'est bon

Posté par re : Couplage de ressort 18-02-14 à 13:19

Pourquoi ?
Puisque si on exerce un déplacement x2 vers la droite le ressort kC se comprime donc la force de rappel devrait être dans l'autre sens aussi ?

Ce topic

Imprimer
Réduire / Agrandir
Pour plus d'options, connectez vous !
Fiches de physique

Fiches de physique - chimie

Rechercher

Espace membre

Zone membre

Pas de compte ?
Je m'inscris

Changer d'île

Couplage de ressort

Seuls les membres peuvent poster sur le forum !

Ce topic

Fiches de physique