Bonjour
Tu obtiens :
Y_A=a.sin(2.f.t)
Comme tu l'as dit :la vitesse est la dérivée par rapport au temps :
v_A=2.f.a.cos(2.f.t)
Pour la question 2, t doit vérifier simultanément :
sin(2.f.t)=0,5
cos(2.f.t)>0
Si les choses ne te paraissent pas évidentes, tu peux dessiner un cercle trigonométrique.

C'est bon j'ai réfléchis et je m'en suis rendu compte il faut que je prenne la valeur pour laquelle la dérivée est >0 dans ce cas
Sin(160pit)=sin(pi/6)
Donc
160pit=pi/6+2p(pi)  va être la seul valeur avec laquelle je vais pouvoir chercher t car 160pit=Pi- pi/6+2p(pi) donne une valeur négative dans la dérivée

Je fais donc pareil pour la seconde date et pour les valeurs décroissante j'ai juste à prendre les valeurs que je n'ai pas prise précédemment si je comprends bien ?

Si je comprends bien l'énoncé, la seconde date concerne toujours le point A. Par définition de la période, T=(1/f) représente la durée entre deux passage consécutifs de A à la même position et avec la même vitesse. La seconde date est donc égale à la première augmentée de T ; la troisième date serait la première augmentée de 2T et ainsi de suite.
Remarque : tu arriverais au même résultat en écrivant que les dates successives correspondant à Y_A=a/2 avec vitesse positive vérifient :
2..f.t=(/6)+2k.
avec k entier positif ou nul.

Donc la seconde date serait simplement ma valeur de t trouvé précédemment soir ((1+12k)/960 )+T ??
Ou alors je fais sin(160pit+T)=sin(pi/6) ?

Tu n'as pas compris mon message. Si t1 désigne la première date de passage, la deuxième est :
t2=t1+T
la troisième est :
t3=t1+2T
et ainsi de suite avec T=(1/f)

Aaaah d'accord désolé j'ai mal compris ,j'ai un peu du mal à me représenter les choses c'est pour cela que je m'entraîne.

Bon donc j'ai t2=t1+T
Donc t2=(1+12k/960)+1/80
Puis je réduis

D'accord

Dans un second temps j'aimerai vraiment qu'on m'aide pour la dernière question lorsque je dois tracer l'allure de la courbe à différents instants.

Je l'ai fait mais je penses que j'ai faux

J'ai chaque fois calculer la distance AB à différents instants

Ex : à t=0 , A et B sont confondus

À t=2 on a xB-xA = ct2 donc 0,7cm donc chaque point de la courbe doit être reculé de 0,7cm

Cependant on me demande de vérifier l'élongation et je ne vois pas comment je peux faire ca ???

Pour la question 3, puisque l'amortissement est négligé, il faut considérer qu'un point d'abscisse x reproduit le mouvement de la source A avec un retard égal à (x/c). A la date t, le point d'abscisse "x " a l'ordonnée qu'avait A à la date (t-x/c). Il suffit donc de reprendre l'expression de y_A et d'y remplacer t par (t-x/c).


avec :
longueur d'onde :

Oui ca j'ai précisé que je l'avais fait je trouve alors t1= -3  t2= 3 et t3=-1,2*10^-12 d'ailleurs le résultat de t3 me paraît bizzar.

Mais c'est la suite de la question qui me pose problème car on me demande de le représenter graphiquement et de vérifier l'élongation et c'est cela que j'ai du mal à faire

Question 3 :
pour l'aspect de la corde à une date t donné : remplace t par sa valeur numérique dans l'équation que je t'ai fournie. Tu obtiens alors y en fonction de x. Cela te donne une sinusoïde de période égale à la longueur d'onde ;


où K est une constante à t donné.

D'accord si j'ai bien compris je remplace dans la formule avec la valeur de t numérique puis lambda est la période ici 20 cm.
Pour vérifier l'élongation sur le graphe comment je m'y prends?
J'ai l'impression de ne pas bien comprendre

Pour t'aider un peu, voici, représentées sur les cinquante premiers centimètres, l'aspect de la cordes représentée aux trois dates :
0 ; 0,04375s ; 0,059375s
A toi de réfléchir et de les identifier !

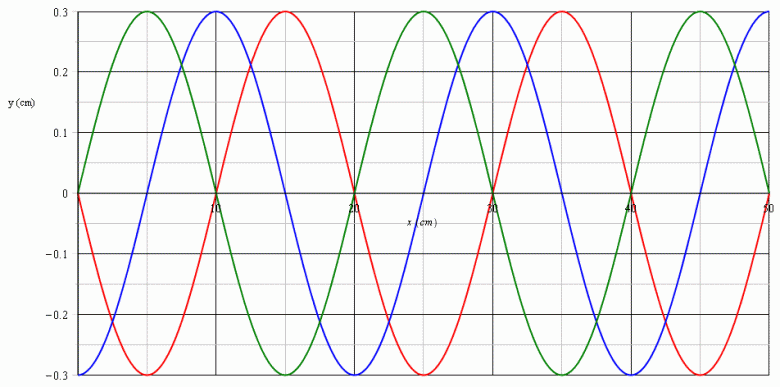
Je comprends la période spatiale de 20cm , je comprend l'amplitude de 3 mm je comprends la sinusoide mais malheureusement je ne comprends pas comment vous avez fait pour connaître l'allure c'est à dire par exemple pour connaître que la valeur max de la courbe bleu était atteinte pour x=10 cm alors que les autres s'y annulait ??? Pouvez vous m'éclairer

C'est bon j'ai compris !!!! Merci beaucoup il suffit de rendre des valeurs remarquables par exemple pour t=0

On a 3sin((-2pi)*x/lambda)=0
Donc sin((-2pi)*x/lambda)=0
Puis on resouds comme une équation trigonométrique
Grâce à ca je peux dire que la courbe verte est celle de t=0

Ais -je bien compris ??

Enfait je ne penses pas avoir compris car je suis bloqué je trouve des valeurs négatives de x
Par exemple pour 3sin(-2pi*x/l)=3
On a  sin(-2pi*x/l)=sin(pi)
Or j'aboutie a un résultat négatif de x=-5-20kpi