Bonjour
Je suppose que, dans un repère terrestre supposé galiléen, le point de fixation de la corde à l'avion décrit une trajectoire de centre A, de rayon R avec une vitesse horizontale V=R. ; cette vitesse intervient certainement dans la résolution du problème. La trajectoire de A appartient à un plan horizontal (altitude fixe).
Essaie de faire une figure en représentant les forces appliquées à la masse m de poids P fixée à l'extrémité inférieure de la corde ; fais bien attention à l'inclinaison de la corde. Tu te poseras alors une question : est-il réaliste d'imaginer que la masse reste immobile par rapport à la terre ?

Bonjour,
Il s'agit que la partie lestee reste immobile par rapport au sol  afin qu'une personne puisse la toucher par exemple.
Cordialement

Nous sommes bien d'accord !
Suis dans ces conditions mes remarques de 16h01 et réfléchis à ma dernière phrase !

Si c'est bien cela ton énoncé ...

Alors achète un hélicoptère.

Il me semble que tu n'as pas fait ce que je t'avais suggéré, soit  :

"Ecris l'énoncé tel qu'il t'a été donné et pas l' interprétation que tu en as faite."

  Ma phrase a ete mal ecrite. L'avion decrit un cercle horizontal, mais toujours le meme.
  L'avion reste en permanence au dessus d'un meme point.

J'ai bien peur qu'il ne s'agisse pas d'un exercice mais d'une situation physique imaginée par capitainecook... D'où la nécessité de réfléchir au réalisme de la situation !
On voit fréquemment, surtout en montagne, des hélicoptères transporter de lourdes charges au bout d'un câble. Comment s'oriente le câble lorsque l'hélicoptère décrit un virage par rapport à la terre ?

Bonjour capitainecook
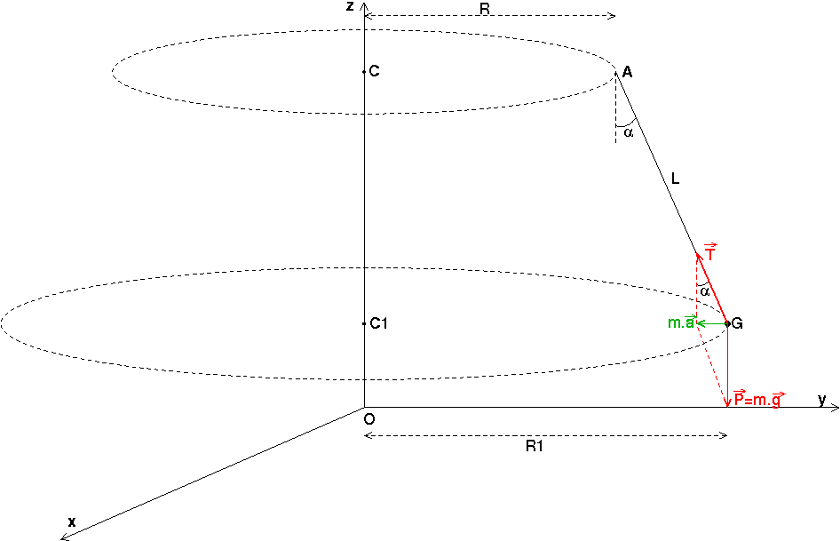
Pour t'aider à comprendre pourquoi ton hypothèse sur une charge immobile par rapport à la terre est physiquement irréaliste, je t'invite à regarder le schéma ci-dessous. Les mouvements sont étudiés par rapport à un repère (Oxyz) fixe par rapport à la terre, donc considéré comme galiléen. L'axe (Oz) est vertical. L'extrémité supérieure A de la corde de longueur L est animée par rapport à ce repère d'un mouvement circulaire uniforme autour de l'axe (Oz) à la vitesse angulaire . Le centre fixe de la trajectoire de A est C, le rayon de la trajectoire est R.
On se limite à l'étude de la corde lorsqu'elle est inclinée d'un angle fixe par rapport à la verticale, la corde restant constamment dans le plan mobile contenant l'axe (Oz) et le point A. Le centre G  de la charge est donc aussi animé d'un mouvement circulaire autour de l'axe (Oz) de vitesse angulaire , de rayon R1, de centre C1. Cette charge est soumise à deux forces :
Son poids et la tension de la corde. Si on note le vecteur accélération de G, la relation fondamentale de la dynamique appliquée à la charge conduit à :


Tu connais sûrement les propriétés du vecteur accélération de G en mouvement circulaire uniforme de rayon R1 et de centre de trajectoire C1 : ce vecteur est un vecteur normal centripète de norme a=R₁.², sa direction est à chaque instant celle de la droite GC1 et il est constamment orienté vers C1.
Regarde bien la figure : pour que le vecteur soit normal centripète, la corde doit nécessairement être inclinée vers l'extérieur : plus précisément : R1 > R ; Dans ces conditions, il est bien sûr impossible que G puisse être immobile par rapport à la terre.
Remarque 1 : si cela t'intéresse, tu peux faire une mise en équation de la situation qui te conduira à exprimer le rayon R1 en fonction de R, , L et g. Je te laisse réfléchir calmement à la situation et proposer une solution si cela t'intéresse.
Remarque 2 : Il aurait été possible de raisonner dans un repère tournant autour de l'axe (Oz) à la vitesse angulaire . Dans un tel repère, A, G et la corde sont fixes mais ce repère n'est pas galiléen. Il faut alors ajouter un terme correctif aux forces réellement exercées sur la charge : la pseudo-force d'inertie centrifuge. On aboutit au résultat recherché en écrivant que la charge est en équilibre sous l'action de son poids, de la tension de la corde et de la pseudo force d'inertie centrifuge. Le calcul n'est pas plus simple et il n'est pas sûr que cette notion de pseudo force d'inertie soit à ton programme...