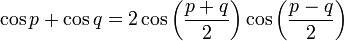Bonjour , pour la préparation d'un tp je dois montrer que
" u = 2u₀.sin(kx).sin(t).e ".
Voici l'énoncé

Nous étudierons le phénomène de résonance à l'aide d'un dispositif
simple, connu sous le nom de corde de Melde. Il est constitué d'une
corde de longueur l tendue entre une poulie et un vibreur, à l'aide
d'une masse m. Le vibreur génère une onde correspondant au
déplacement vertical de corde. Il est alimenté par un générateur bassefréquence
permettant de fixer la fréquence de l'onde. L'onde se
propage du vibreur vers la poulie où elle subit une réflexion totale. La
corde est donc soumise à deux ondes, l'une se propageant du vibreur
vers la poulie et l'autre (réfléchie) de la poulie vers le vibreur.

Lorsque l'on impose une réflexion totale à une onde propagative
monochromatique il se forme une onde dite stationnaire présentant des
noeuds (amplitude nulle) et des ventres (amplitude maximale) de
vibration. Cette appellation d'onde stationnaire vient du fait que ces
noeuds et ces ventres de vibrations ne se déplacent pas en fonction du
temps. Ceci peut se montrer en calculant la somme de l'onde incidente
et réfléchie
u₁ =  u₀cos(t + kx).e

et

u₂cos(t - kx + ).e  


L'axe x étant orienté de gauche à droite. Le déphasage de π vient de la
condition aux limites appliquée au niveau de la poulie, assurant que
l'amplitude de déplacement y est nulle.
Montrer que l'onde résultante est donnée par

u = 2u₀.sin(kx).sin(t).e


avec u1, u2, u, e vecteurs.

Je ne vois pas du tout comment arriver à ce résultat si u = u1 + u2.

Merci d'avance pour toute aide