Bonjour à tous,

Je bute complètement dans un exercice où il faut trouver les coordonnées du vecteur poids de l'objet, dans 2 référentiels différents (je n'ai donc pas eu le temps de faire les autres questions vu que je bute déjà sur la question 1, je vais quand même mettre toutes les questions de l'exo, vu que si je réussis à comprendre la question 1, sans doute j'arriverais peut-être à faire les autres questions, mais déjà si je pouvais réussir à comprendre comment résoudre la question 1, ce serait bien).

J'ai fait des croquis pour essayer de comprendre et faire des angles égaux partout pour m'aider, mais sans résultat.
Je vais mettre ces croquis ci-dessous pour que l'on comprenne mes raisonnements.

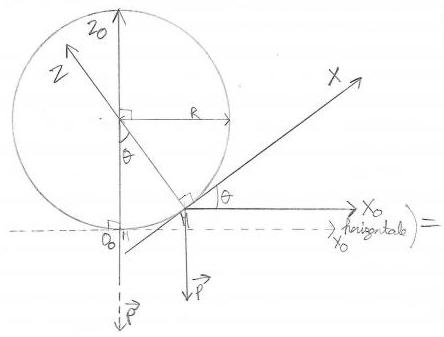
Mais d'abord voici la figure de l'énoncé posé ci-dessous en premier avec le titre "énoncé figure" qui est la référence pour toutes les questions de l'exercice.

Enoncé de l'exercice

"Un avion de masse m effectue une trajectoire en arc de cercle (cercle de centre 0, de rayon R) représenté sur la figure de l'énoncé (voir "énoncé figure"). Sa vitesse est supposée constante en norme V. L'avion est représenté par le point matériel M.
On utilise 2 repères de représentation:
-Le repère orthonormé (O, Xo, Zo) galiléen liée au sol.
- Le repère orthonormé (M, X, Z) lié à l'avion, X est tangent à la trajectoire à l'instant t et fait un angle (t) avec l'horizontale Xo.

(Remarque sur  la figure de l'énoncé on constate un point non mentionné dans l'énoncé de l'exercice, c'est le point 0o qui est l'intersection entre Zo et le cercle, et dont la tangente perpendiculaire à Zo est parallèle à Xo, on sait seulement que 0o peut être le point M aussi, vu que le point M se situe sur tous les points du cercle).

Questions de l'énoncé :

1) Exprimer le vecteur Poids de l'avion dans chacune des 2 bases orthonormés (Xo,Zo) et ( X,Z)

Là la question au quel je bute, j'ai mis 2 croquis ci (dessous pour répondre pour la base (Xo,Zo), et le deuxième pour répondre à la base (X,Z).

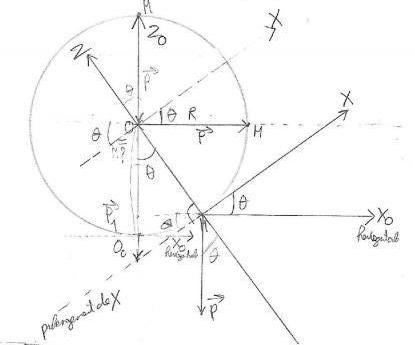
-Pour la base (Xo,Zo), j'ai fait 2 translations, d'abord la translation de Xo pour qu'il soit à la fois  perpendiculaire à Zo (parce que oui, bizarrement dans l'énoncé, le Xo et le Zo sont détachés l'un de l'autre)  et également parallèle au Xo de l'énoncé qui fait un angle avec le X de l'énoncé. Puis ensuite j'ai fait la translation du vecteur P du point M, j'ai décidé que 0o devenait le second point M (vu que tous les points du cercle sont M) et surtout puisque 0o est déjà sur la droite Zo, et j'ai prolongé la droite Xo pour avoir le référentiel (Xo,Zo) décalé vers la gauche. Le seul problème c'est l'origine 0 qui se trouve tout en haut, c'est comme si j'avais translaté l'origine 0 en 0o vers le bas au croisement de Zo et Xo.
Enfin, comme le vecteur P de M point du cercle est verticale et descendant, et que le vecteur P de 0o point du cercle est verticale et descendant et situé sur la droite Zo, j'ai dit que P dans la base (Xo,Zo) s'exprime: P= -mgzo

- Pour la base (X,Z), alors c'est là que cela devient super compliqué. Je me suis mis à chercher des angles égaux à partout pour essayer d'avoir un vecteur P de M cosinus ou sinus avec une des droites X ou Z.

Mais cela n'a pas marché.

Alors j'ai essayé de faire des vecteurs égaux à P de M partout, mais je me suis demandé si j'avais le droit de faire cela et dans quels cas je pouvais le faire...

Par exemple pour X j'ai imaginé de translater le vecteur P de M et de faire le vecteur P de 0 à la place, de prolonger le X pour avoir un sinus de
Mais là, rien ne garantit que le vecteur P de 0 soit égale en longueur au P de M, même si là, c'était le seul moyen d'avoir un sinus de facile avec l'angle P et l'un des axes. Je l'avais donc exprimé: sin=- X/P1 (car le X a été prolongé à partir de l'origine du repère M pour avoir le sinus de , donc on est dans les négatifs)

P1= P donc P= -mg sinx


Pour Z, j'ai pris un P du point M tout en haut du cercle,  
puis j'ai dit cos= -Z/P
donc Z= - P cos
donc vecteur P selon Z= - mg cosvecteur z

J'ai donc dit que la réponse totale du vecteur P de M dans le repère (X,Z) est :
-mg sinvecteur x- mg cos vecteur z

Mais voilà cela semble fouilli tout cela,  je ne sais même pas si j'ai bon ou si j'ai bien raisonné, donc si certains  ont le temps de jouer les pères Noel de physique et  de m'expliquer comment bien raisonner et bien expliquer la réponse à la question 1 avec des croquis ou des schémas ce serait vraiment le plus beau joli cadeau de Noel...

2) Pourquoi le référentiel lié à l'avion n'est pas galiléen

Ma réponse à la question 2:  comme l'avion a un mouvement circulaire de rayon R , et que le référentiel galiléen doit être soit fixe soit rectiligne, l'avion forcément n'est pas galiléen...)

3) Exprimer le vecteur OM  dans chacune des bases (Xo, Zo) et (X,Z).

(là j'ai l'impression que je vais faire les mêmes réponses que j'ai trouvé pour le vecteur P de M avec ma translations du vecteur P  donc je vais buter autant dans la question 3 que je l'ai déjà fait dans la question 1...)

4) Déterminer l'expression du vecteur vitesse  du point M dans (Xo, Zo), et (X,Z)

Bon, là je crois avoir bon:
comme le vecteur vitesse est tangent à la trajectoire, déjà il y a dans (X,Z), le vecteur vitesse M est confondu avec  X, donc VM dans (X,Z)= V  X et donc dans la base (Xo, Zo), VM= Vcos Xo  + V sinZo

5) Déterminer l'expression du vecteur accélération du point M dans (Xo, Zo) et (X,Z)
Là, j'ai dérivé les résultats trouvés à la question 4, donc le vecteur  A (accélération) M=V pour (Xo,Zo) et dans le repère (X,Z) le vecteur A (accélération) de M= Vcos + V sin

Voilà Merci à tous d'avoir lu, et aussi j'ose espérer que c'est possible pour m'aider à résoudre cet exercice, et à bien comprendre où j'ai faux et les tracés inutiles que j'ai fait dans les 2 derniers croquis qui sont en dessous de la figure de l'énoncé dans ma quête interminable de trouver les coordonnées de vecteur Poids du point M dans les 2 bases (Xo,Zo) et (X,Z).

En attendant, je vous souhaite un Joyeux Noël à tous!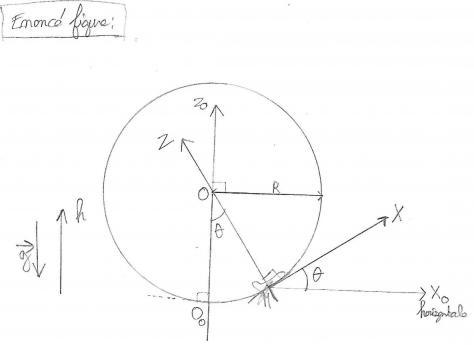







_____

***Images recadrées***