coordonnées cinématique mécanique : exercice de sciences physiques de maths sup

 Niveau maths supPartager :
			        
coordonnées cinématique mécanique
Posté par 
Debc  15-10-17 à 18:21
Bonjour à tous ! Alors voilà j'ai besoin d'explications sur quelque chose d'assez basique. Il s'agit d'exprimer les coordonnées. Je n'avais aucun problème avec les simples qu'on voit en terminale (il suffisait d'utiliser "sohcahtoa") mais là j'ai plus de mal je n'arrive pas à comprendre. Voici un exemple:
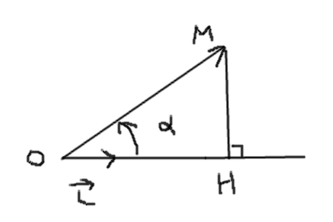
En se reportant à la figure, exprimer les coordonnées x,y,z du point M en fonction de r,,.
J'ai les réponses mais je ne les comprend pas.

Merci d'avance pour votre aide ! 

***Image recadrée***
 Posté par 
amelie3317re : coordonnées cinématique mécanique  15-10-17 à 18:30
Bonjour.

Projette le vecteur  sur l'axe (OZ) ; cela te donne z en fonction de r et theta.

Projette  sur la droite (OH) et ensuite tu projettes cette projection sur les axes (Ox) et (Oy).

Tu obtiens alors x et y en fonction de r theta et phi.
 Posté par 
diracre : coordonnées cinématique mécanique  15-10-17 à 18:33
Hello

Chasles et Pythagore sont tes amis:

Chasles te dit aussi:

Pythagore te dit ensuite:

 Posté par 
diracre : coordonnées cinématique mécanique  15-10-17 à 18:33
Ooopppsss désolé Amelie3317 
 Posté par 
amelie3317re : coordonnées cinématique mécanique  15-10-17 à 18:50
Petit (rappel ?) sur l'interprétation géométrique du produit scalaire.

 vecteur unitaire

Le produit scalaire  est égal à la mesure algébrique 

D'autre part le produit scalaire  = 

Donc  .

 Posté par 
amelie3317re : coordonnées cinématique mécanique  15-10-17 à 18:53
Évidemment si on projette  sur l'axe (Oz) on obtient la même composante sur  que "dirac".

A chacun ses préférences.

A "debc" de voir.
 Posté par 
amelie3317re : coordonnées cinématique mécanique  15-10-17 à 18:54
Et pas de soucis "dirac", ce qui compte c'est que "debc" avance. 
 Posté par 
diracre : coordonnées cinématique mécanique  15-10-17 à 18:58
Citation :
Le produit scalaire  est égal à la mesure algébrique  

Pas tout à fait  dans le schéma proposé par Debc

Mais c'est un fort en coquilles qui fait ce commentaire  
 Posté par 
amelie3317re : coordonnées cinématique mécanique  15-10-17 à 19:08
Ce sont mes notations qui ne sont peut-être pas très adaptées.

Mon repère n'a rien à voir avec celui de debc.

Je lui propose un rappel très général pour qu'elle puisse le transposer dans le repère cylindrique qu'elle propose.
 Posté par 
Debcre : coordonnées cinématique mécanique  15-10-17 à 19:16
ah j'ai compris ! merci énormément Amélie ! Je faisais vraiment un blocage là-dessus
  Posté par 
Debcre : coordonnées cinématique mécanique  15-10-17 à 19:16
Oups je viens de voir toutes les réponses qui sont arrivées en même temps (je n'avais vu que la 1ère réponse quand j'ai répondu) donc merci à vous 2