Inscription / Connexion Nouveau Sujet
Coordonnée et vitesse
Bonjour,
Je sais que la dérivée de la position.
Ainsi, pour le pendule je détermine la position puis je la dérive par rapport au temps pour avoir la vitesse.
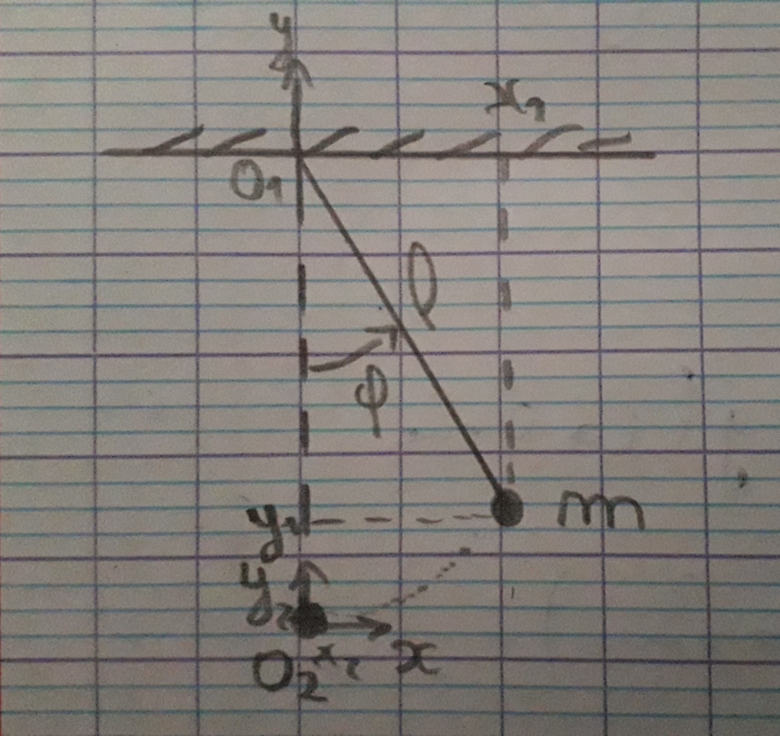
Pour l'origine O1, pas de soucis, je prends un cas très général: x1=l.sin(phi) et y1 =-l.cos(phi)
v1x=l.(d(phi)/dt).cos(phi) et v2x=l.(d(phi)/dt).sin(phi)
Et donc v2=l.(d(phi)/dt)
Maintenant pour l'origind O2, dans le cas particulier où la masse coïncide avec l'origine:
x2=0 et y2=0 et donc v2=0. Or on sait qu'à cet endroit la vitesse est maximale.
Alors on n'a pas le droit de choisir l'origine dans le cas particulier où l'objet étudié s'y trouve ?
Maintenant l'origine O1 pour étudier le cas particulier où la masse se trouve à O2: x=0 et y=-l et donc v2=0, même remarque.
Hello
x2=0 et y2=0 et donc v2=0
Le donc est un peu audacieux
Par ailleurs, ton expression de la vitesse contient une coquille: en fait
Je t'engage à exprimer la conservation de l'énergie mécanique pour retomber rapidement sur tes pieds
Oui en effet pour la coquille.
x2=0 et donc sa dérivée par rapport au temps est également nulle, idem pour y2.
Pour O2 en origine, l'Epp est également nulle.
Pour la conservation de l'énergie:
1)dE/dt=0 cela n'apporte rien
2) soit le point A à O2 et le point B au cas "général"
Em(A)=Em(B)
0=(1/2)ml2(d(phi)/dt)2 + mg(l-lcos(phi))
Hum hum,
"x2=0 et donc sa dérivée par rapport au temps est également nulle"
Je maintiens, avec bcp de gentillesse, que le "et donc" est audacieux (et faux en fait)
Prenons un exemple simple:
on dérive
donc à chaque fois que x=0 on peut dire que dx/dt= +1 ou -1
Cela t'éclaircit il les idées?
Oui un peu, que faut-il faire dans cette situation ?
Peut-on déterminer autrement la coordonnée de x pour faire apparaitre explicitement le temps ?
On n'a pas le droit de choisir l'origine dans le cas particulier où l'objet étudié s'y trouve ?
Re hum hum 
"que faut-il faire dans cette situation ? "
je ne sais pas trop ce qu'il y a à faire ni de quelle situation tu parles
"déterminer autrement la coordonnée de x pour faire apparaitre explicitement le temps ? "
Dans ton premier système de coordonnées
tu as bien établis et
Si je comprends bien tu veux te débarrasser de pour établir une fonction
explicite du temps?
Pour le faire je t'engage à:
- exprimer la valeur de l'énergie potentielle
- celle de l'énergie cinétique
- exprimer que l'énergie mécanique se conserve (dEm/dt = 0)
Ce qui te fournit une équation différentielle du 2nd ordre en
Ce qui t'interesse (enfin j'espère car sinon c'est plus compliqué) c'est l"expression au voisinage de ce qui embarque
petit et permet d'approximer
par
pour résoudre une version simplifiée de l'équation différentielle et ainsi établir la loi horaire de
Après il n'y à plus qu'à injecter dans l'expression de
De mon côté, je "vois" via un autre post que tu viens d'actualiser que le sujet ne t'est pas inconnu, tu devrais rapidement retomber sur tes pieds, surtout qu'avec vanoise (que je salue bien) tu disposes déjà d'un soutien ... brillant
Bonsoir à toi gbm et à tous les iliens assidus ... bcp de boulot ces derniers mois qui m'a maintenu au large 
Bonjour dirac,
Effectivement, les derniers mois ont été particulièrement singuliers et prenants ... Aussi bien ici, qu'au niveau boulot et perso .
Tu verras que l'
continue son bonhomme de chemin, avec la poursuite du chantier fiches (classe de seconde finie, classe de première presque finie - plus que 2 fiches - et classe de terminale en cours). La FAQ a également été mise à jour pour tenir compte du retour d'expérience de ces derniers mois, de même que les motifs d'avertissement.
L'activité sur l'île a été conséquente de mars à juin, plus calme depuis.
Bon WE !
Annuler
connectez vous