Inscription / Connexion Nouveau Sujet
Contrainte Holonômes /\ Mécanique Analytique
Bonsoir,
J'aurais besoin d'éclaircissements sur la notion de contraintes holonôme en physique analytique, en lagrangien plus précisement...
Donc, j'ai à peu près compris la définition formelle du cours, manquerait que l'application concrète sur un exo je pense !
Je vous adjoint ci-dessous la définition qu'on m'a donné, ca peut peut-être aider ! 
Soit N particules indépendantes dans le repère fixe, Galiléen. Chaque particule à 3 degrés de liberté, et le système a donc 3N dégrés de liberté.
On les notes .
Les contraintes entrainent une diminution de ce nombre de degrés de liberté.
Si les conditions de liaison s'exprimment sous la forme d'une équation du type :
avec i
[1;]. La contrainte est holonôme.
Ces équation permettent d'exprimmer des 3N coordonnées
en fonction des
autres coordonnées qui sont alors indépendantes.
Donc, aprés avoir vu cela en cours, et fait quelques calculs de Lagrangien ''simples'', je bloque sur un exercice ou apparaissent ces fameuses contraintes ! :s
Voici l'exo :
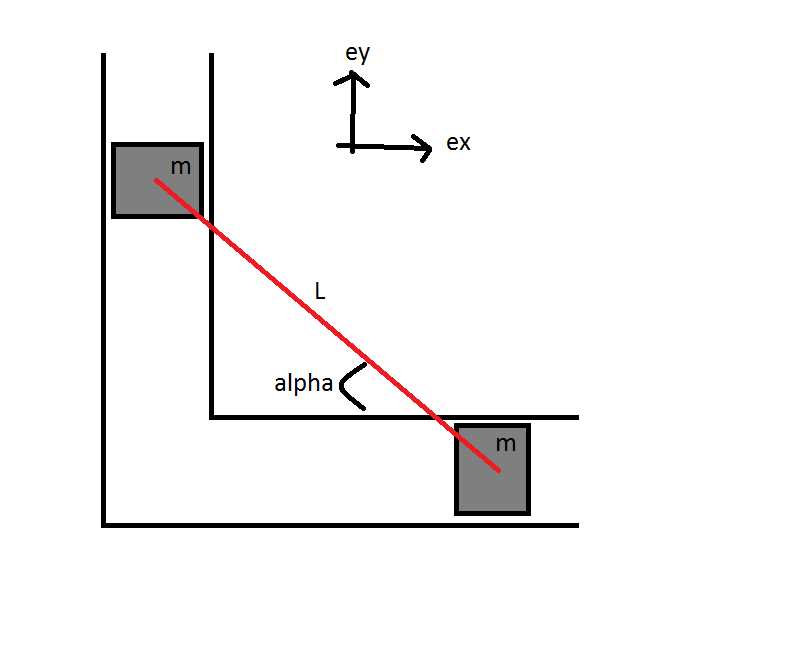
Deux blocs de même masse sont reliés l'un à l'autre par une barre rigide de longueur fixe L (on néglige la masse de la barre). Les deux blocs se déplacent sans frottements le long d'un chemin prédéfini par des parrois. Le système est soumis au champ de pesanteur terrestre.
On me demande de calculer le Lagrangien en fonction des masses, de L et d'
!
Donc L = T - V, etc...
De ce que j'ai compris du cours, j'ai ici 2 contraintes exercées sur mon système :
- La contrainte impliquant que la distance entre mes deux masses est constante égale à L.
- La contrainte impliquant que mes deux masses sont obligées de se mouvoir dans le chemin prédéfini par les parois.
Mais là ! PLUS rien, aucune idée de comment procéder pour exprimer cela mathématiquement !
J'imagine que la masse sur la partie horizontale aura une énergie potentielle nulle par rapport à l'autre.
Quand celle sur la partie verticale se déplace (grâce au poids), l'autre suit le mouvement sans opposer de résistance, car pas de frottement, et liée rigidement, donc on aurait la vitesse de le premier bloc qui entraine une vitesse égale sur la second bloc ?
Mais comment calculer cette vitesse, car elle est obligatoire dans le calcul de T....
Donc voila, merci de votre aide, j'espère avoir été clair....!
Bonjour
Cette branche de la mécanique est un peu "ancienne" pour moi et j'ai sûrement besoin de revoir mon cours sur le sujet ! Un peu d'aide tout de même.
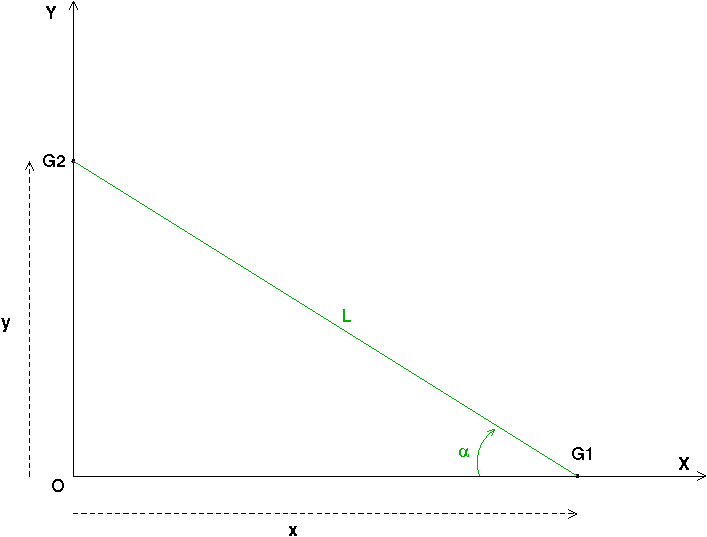
Tu peux poser q1=x ; q2=y ; L'existence de la liaison permet d'exprimer ces deux inconnues en fonction de la seule variable .
q1=L.cos() ; q2=L.sin() ;
dq1/dt=-L.(d/dt).sin()
dq2/dt=L.(d/dt).cos()
Les seuls variables du problèmes sont et sa dérivée par rapport au temps...
Sous toutes réserves...
Je pense ne pas t'avoir orienté sur une fausse piste car le principe de moindre action conduit de façon très élégante à l'équation différentielle suivante :
L.(d2/dt2)+g.cos()=0.
Remarque : vue la simplicité du dispositif, un raisonnement sur la conservation de l'énergie mécanique conduit presque aussi rapidement au résultat mais j'ai bien compris que le but de cet exercice est de te familiariser avec le formalisme lagrangien pour aborder ensuite des problèmes plus complexes...
Bonsoir,
Non, je vois pas d'ou sortirais ma vitesse ....
On peut considérer q1 et q2 comme des positions, et donc les dériver par rapport au temps ?
q1 et q2 sont effectivement les coordonnées non nulles de G1 et G2 les centres d'inertie des deux solides ; leurs dérivées par rapport au temps sont les vitesses.
Je t'ai déjà posé presque tous les calculs. Il est immédiat d'obtenir en fonction de L, g,m, et d/dt l'énergie cinétique et l'énergie potentielle du système. La suite est facile...
Yes ! Je retombe enfin sur cette equa diff ! Saloperie de relation trigonométrique, suffit de la louper et on se retrouve avec des calculs interminables ! 
Cependant, mon énoncé me demande d'avoir une eq.diff sous la forme
1/2 (d/dt)² + g/L sin((t)) = constante.
C'est faisable en partant de la première qu'on a trouvé ? Sans forcément donner la réponse, juste histoire de savoir si je pars dans le bon sens ou pas
Pour obtenir une expression intégrée de l'équation différentielle, une méthode simple consiste souvent à multiplier chaque terme par la dérivée première par rapport au temps de la variable : d/dt. Retiens bien cette méthode, elle devrait te servir souvent !
Cela donne :
L.(d/dt).(d2/dt2)+g.(d/dt).cos()=0
Tu prends ensuite une primitive de chaque terme :
primitive de : L.(d/dt).(d2/dt2) : ½ L.(d/dt)2
primitive de : g.(d/dt).cos()=g.sin() ; cela te conduit bien à l'expression recherchée. Cela dit, pour obtenir directement cette constante, il suffit d'écrire que l'énergie mécanique est une constante puisque :
Ec=T=½m.L2.(d/dt)2
Ep=V=m.g.y=m.g.L.sin()
Mais le but de cet exercice est d'apprendre à utiliser le formalisme Lagrangien en commençant par des situations très simples. Tu vas avoir l'occasion plus tard dans le programme de vérifier l'efficacité de ce formalisme dans des situations plus complexes...
Bonsoir,
J'aurais jamais pensé à multiplier puis intégrer chaque termes ! Merci pour le coup de main ! Mais forcément, une fois multiplié par la dérivée d'alpha, ca saute aux yeux !
Merci beaucoup pour cette aide, ça m'a beaucoup éclairé sur la méthode de résolution des systèmes contraints "simples" !
Bonne soirée !!
Annuler
connectez vous