Inscription / Connexion Nouveau Sujet
construction de Descartes
Bonjour,
J'ai un exercice que je ne parvient pas à résoudre:
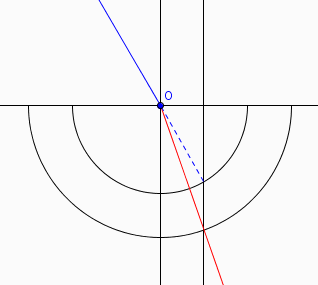
Soit un dioptre plan D séparant deux milieux d'indices respectifs n1 et n2. Un rayon incident Ri, dans le milieu d'indice n1 et d'angle d'incidence i1, coupe D en O. Tracer le cercle C1, de centre O, de rayon n1I0 (où I0 est une longueur d'unité arbitraire) et compris dans le plan d'incidence, ainsi que le cercle C2, de centre O, de rayon n2I0 et compris dans le plan d'incidence.
Soit P le point d'intersection du cercle C1 et du prolongement du rayon Ri (P est dans le milieu d'indice n2).
Soit Q le point d'intersection du cercle C2 et de la droite perpendiculaire au dioptre D passant par le point P (Q est dans le milieu d'indice n2).
1. Montrer que la demi-droite [OQ) est le rayon réfracté.
j'ai fais un schéma mais je n'arrive pas à le démontrer, je pensais utiliser la loi de Snell-Descartes mais je n'obtient rien.
2. A quoi correspond le cas où la perpendiculaire à D passant par le point P ne coupe pas le cercle C2?
Merci de votre aide
i1 est l'angle bleu
i2 est l'angle rouge
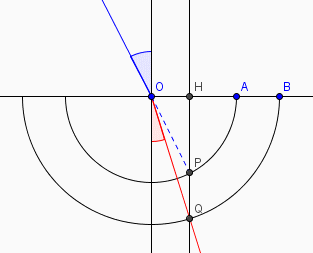
Quelles sont les mesures des angles et
?
OA = n1
OB = n2
Alors ?


mesure de = i1
mesure de = i2
OP = OA = n1
OQ = OB = n2
OH = OP.sin() = OQ.sin(
)
donc
n1.sin(i1) = n2.sin(i2)

mais oui! merci beaucoup
juste une précision j'ai le droit d'écrire qu'une longueur est égale à l'indice d'un milieu (OP=n1)
par contre je ne vois pas pour la question 2, parce que si la perpendiculaire à D passant par le point P ne coupe pas le cercle C2 on a le rayon OP non?
Il est plus correct d'écrire, comme dans l'énoncé OA = n1.L0
L0 étant une "longueur arbitraire"
____________
Avec la figure actuelle il est sûr que la perpendiculaire à D passant par P coupera toujours le cercle C2
Que faut-il faire pour que la perpendiculaire à D puisse ne pas couper le cercle C2 ?

Cela donnerait en effet le rayon réfléchi, mais ce n'est pas la question posée.
Dans quelle condition la perpendiculaire à D passant par P peut ne pas couper le demi-cercle de rayon n2.L0 ?
Tu n'as plus aucun souvenir de l'optique faite au lycée ?

Oui, de réfraction limite qui est donc suivi de la réflexion totale.
Quelles sont les conditions pour que cela ait lieu ?

Es-tu sûr ?
n1 < n2 : c'est le cas de la figure que j'ai postée. Or il est évident que dans ces conditions la perpendiculaire à D passant par P pourra toujours couper le demi-cercle de rayon n2.L0
Alors que si n1 > n2...

ah oui si j'ai n2>n1 j'ai P qui est situé sur le cercle extérieur je peux alors construire la perpendiculaire qui ne passe pas par Q et j'obtient le rayon incident pour la réfraction limite
J'ai dit "oui" un peu vite :
Oui, si n1 > n2
Pas en entrant dans un milieu plus réfringent qui est le cas de la figure ; mais en entrant dans un milieu moins réfringent.