Inscription / Connexion Nouveau Sujet
Construction d'un champ de contrainte.
Bonjour tout le monde,
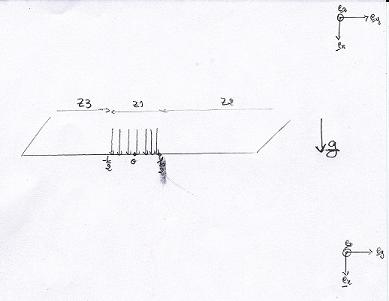
on considère un plan infini selon ey et ez (vecteur normal au plan du pc; désolé pour la mauvaise qualité de l'image). Dans la zone définie par x=0, -L/2
yL/2, z quelconque (notée Z1 e pièce jointe), on applique une force de pression p constante. Les zone y
B/2 et y-B/2 sont libre d'efforts. Il s'agit de construire un champ de contrainte statiquement admissible. Je choisis de construire un champ de contrainte dont la matrice dans la base cartésienne est diagonale.
La continuité du vecteur contrainte se traduit dans Z1 par 
1.(-ex)=pex et dans Z2 et Z3 par 2.ex=0 et 3.ex=0
En écrivant la loi locale d'équilibe : div()+
g=0, j'obtiens dans la zone 1 xx1(x)=-gx-p.
Dans les zones 2 et 3, j'obtiens xx2=-gx et xx3(x)=-gx.
Pour les autres composantes de j'obtiens seulement : yyi =yyi (x,z) , et zzi=zzi(x,y) .
Je me demande si je peux choisir les zzi et yyi nulles.
Bien cordialement.
Edit Coll : image recadrée
Bonsoir,
ça fait un petit moment que j'ai pas refait de MMC mais je vais quand même essayer de t'apporter un autre point de vue sur ton problème.
d'après ton schéma, tu es clairement en présence de contraintes planes dans . Là déjà ça devrait t'aiguiller sur la manière de procéder.
Ensuite, si tu projettes ton équation d'équilibre sur tu devrais trouver
donc yy et zz constants et les conditions aux limites en y et en z devraient te permettre de conclure que les constantes sont nulles.
j'espère que ça t'aidera à résoudre ton problème.
Bonne soirée
Ce qui me chiffonne, c'est qu'on ne peut pas considérer une condition limite dans un plan y=cste ou z=cste, parce qu'un tel plan n'appartient pas au milieu continu. Les conditions limites devraient normalement porter sur les vecteurs contrainte qui s'appliquent sur des surfaces appartenant au milieu en question.
Bonjour,
pour rebondir sur ton problème de conditions aux limites, il me semble qu'elles s'appliquent sur la frontière du milieu soit dans ton cas des droites situées à l'infini (donc pas facilement utilisables).
En tout cas, ton but étant de construire un champ statiquement admissible, si l'équation de la statique te donne yy et zz constants, j'imagine que tu dois pouvoir les choisir arbitrairement nuls sans trop te justifier.
Bonne journée.
Annuler
connectez vous