Inscription / Connexion Nouveau Sujet
Constante vitesse
Bonjour,
On étudie la proportion d'isomère Z (espèce A) et E (espèce B) à température constante. Les deux réactions directe et opposée sont du premier ordre.
| t(min) | 0 | 20 | 50 | 80 | 120 | 170 | infini |
| % de A | 100 | 92.5 | 82.3 | 73.6 | 63.7 | 53.8 | 17.1 |
Déterminer la valeur de la constante d'équilibre de la réaction K et les valeurs des constante de vitesse k1 et k-1.
A<->B ( de A vers B k1 et de B vers A k-1)
K=[B]éq/[A]éq=0.829/0.171=4.84
Pour k1 et k-1, je pense qu'il faut utiliser la loi de vitesse intégrée ln[C]=ln[C]0 -k mais je ne vois pas comment faire.
Bonsoir
Il suffit de traduire en équation le fait que la vitesse d'apparition de B dans le réacteur est la différence entre sa vitesse v1 de formation et sa vitesse v-1 de disparition.
Non : tu raisonnes comme si les deux vitesses étaient indépendantes. En notant x, la fraction molaire de A à la date t, un tableau d'avancement te conduit simplement à :
[A]=Co.x ; [B]=Co.(1-x).
Les valeurs de x aux dates t sont fournies par le tableau.
Mon message précédent conduit à :
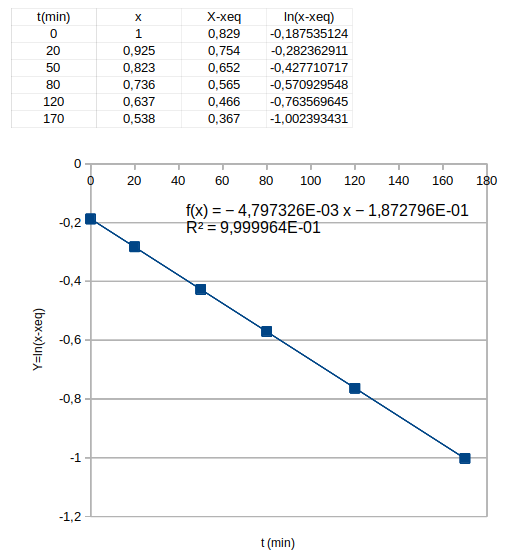
Cela va te conduire à une équation différentielle dont x est une solution très facile à expliciter en fonction de t, de xeq et de (k1+k-1). Il est alors assez facile d'imaginer une courbe à tracer à partir des valeurs de x fournies pour tracer une droite dont le coefficient directeur est -(k1+k-1)... Le tableau de valeurs fournies vérifie tellement bien la théorie que je le soupçonne d'avoir été “arrangé” par le concepteur de l'exercice. Des mesures réelles ne seraient pas aussi précises !
Ayant maintenant la somme des deux constantes de vitesse et ayant obtenue à la question précédente le quotient de ces constantes, facile de terminer !
-d[A]/dt =k1 x.Co -k-1(Co-x.Co)
En integrant, ln[A]=(k1+k-1 -k1.Co).t -ln[A]0 et là il faut faire une régression linéaire ax+b mais je ne vois pas comment déterminer les concentrations.
Comment ai-je obtenu le quotient des constantes à la questions précèdente ?
-d[A]/dt s'exprime en fonction de Co et de dx/dt. Après simplification par Co, tu obtiens une équation différentielle du premier ordre vérifiée par x. Je te laisse faire les calculs. Ces calculs m'ont amené, à l'aide d'un tableur, au résultat suivant. Tu noteras la valeur de R2 extrêmement proche de 1 : la théorie est tout à fait (trop ?) en accord avec le tableau de mesures fourni par l'énoncé.
A toi de faire le raisonnement...
Pour trouver la constante d'équilibre de la réaction K:
K=[B]éq/[A]éq=(m éq(B)/M/V)/(m éq(A)=m éq(B)/méq(A) avec m éq(B)=0.829*m tot et m éq(A)=0.171* m tot donc K=0.829/0.171=4.85.
Et donc, pour utiliser le quotient des constantes:
A l'équilibre, v1éq=v-1éq ainsi, k1[A]éq=k-1[B]éq ; 4.85=k1/k-1
Pour la valeur de k1 et k-1:
Je n'arrive pas à comprendre les étapes qu'il faut effectuées...
Je suis peut-être allé un peu vite... concentre toi sur la résolution de l'équation différentielle vérifiée par x puis sur la méthode graphique permettant d'obtenir la somme des deux constantes de vitesse.
Je vais essayer de te remettre sur les rails sans développer les calculs. Après, en reprenant attentivement mes précédents messages, tu devrais réussir seul. Je repars de :
Cela donne :
Solution de cette équation différentielle du premier ordre :
avec :
sachant que x=1 pour t=0 :
Je pense que tu vois maintenant l'intérêt du tracé que j'ai effectué à l'aide d'un tableur. Tu obtiens directement .
Je te laisse terminer mais le plus difficile est fait.


