Inscription / Connexion Nouveau Sujet
Conservation du flux
Bonjour,
J'aurais besoin de vous afin de comprendre la conservation du flux.
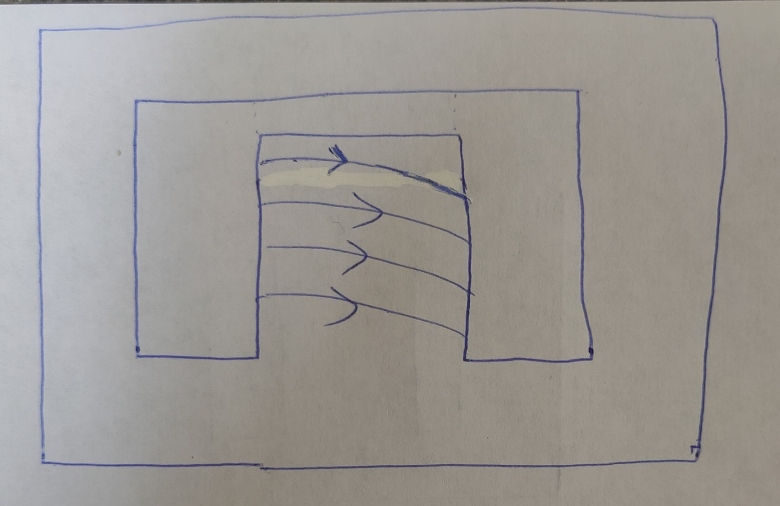
On a le schéma suivant.
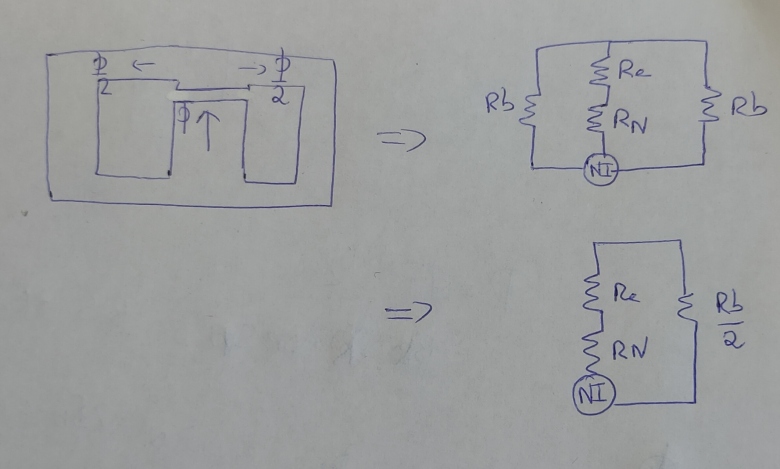
On remplace par les réluctances Rbord, Rnoyau et Rentrefer et la fem.
On trouve son équivalent car Rb est parallèle à Rb (Rb² / 2Rb)
Puis on peut dire que :
Avec Phi1 le flux central et Phi2/Phi3 les flux sur les bords.
Jusqu'à ici je comprends mais après je n'arrive pas à comprendre pourquoi on obtient sur les schémas (normal et son équivalent) :
BeSe = BnSn = 2* Bb Sb Avec Sn = 2Sb donc
Be = Bn = Bb ? Le champ magnétiques est donc le même partout sur les 3 colonnes ... Pourquoi a t on le "2" ?
D'ailleurs savez vous à quoi sert un entrefer dans un circuit ?
Enfin, j'ai une relation non linéaire qui lie B à H sur un hystérésis.
B= μo Hfer + J (Hfer), peut on remplacer cette relation également non linéaire qui depend de l'endroit où on est par
B= μfer Hfer avec μfer non constant sur l'hystérésis (matériaux doux) ? ( μfer etant égal à μo μrfer).
Merci beaucoup !
Bonjour
B= μfer Hfer avec μfer non constant sur l'hystérésis (matériaux doux) ? ( μfer etant égal à μo μrfer).
Je réponds oui à cette question.
Pour ta première question : j'avoue être un peu gêné par tes notations qui diffèrent d'une questions à l'autre et qui ne sont pas celles du schéma.Tu n'aurais pas par hasard un énoncé complet accompagné de son schéma. Dans la mesure où tu as déjà recopié plusieurs lignes de cet énoncé, tu pourrais te contenter de fournir une référence de fichier pdf...
Merci !
Je n'ai pas de schéma. Ce schéma vient d'un TP. Et les formules finales ont été données par les professeurs.
Si jamais on oublie ce que j'ai fait. Comment peut on traiter ici la conservation du flux ?
On voit que le flux dans le noyau est le même que le flux qui passe dans l'entrefer (car sur la même colonne), puis ce flux se coupe en deux flux égaux phi/2.
Ainsi le bord droit voit un flux phi/2 et celui de gauche aussi.
Mais après je n'arrive pas trop à voir...
Si on négliges les fuites magnétiques, on arrive effectivement à ce que tu as écrit.
Si tu connais les aires des sections droites, tu arrives alors à une relation entre les champs d'induction magnétique (B).
Ensuite, l'application du théorème d'Ampère te donne une relation entre les champs d'excitation magnétique (H).
Pour le théorème d'ampère : He* Le + Hd*Ld + Hn*Ln = NI
On peut donc considérer que Hd Ld + Hn Ln = Hfer*Lfer
Pour la conservation du flux, je ferrais :
mais je sais que c'est faux.
Et aussi, je n'arrive pas à me représentation le champ magnétique B, est il le même de chaque côté de Rb ?
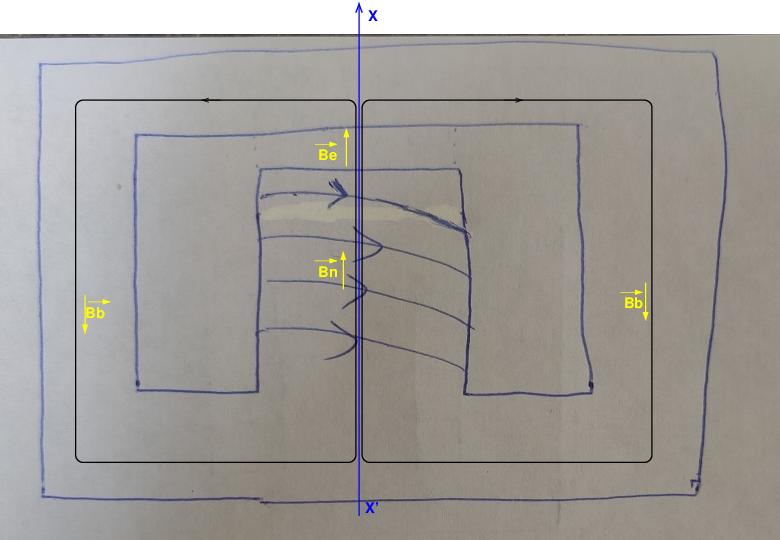
Peux-tu refaire un schéma propre où apparaissent clairement :
*le noyau ferromagnétique et son entrefer ;
* la ou les bobine(s) en précisant l'orientation du ou des courant(s) ?
Impossible, sinon, d'écrire des équations rigoureuses sur le plan algébrique.
En négligeant les fuites magnétiques et en utilisant les notations de tes précédents messages et en supposant le dispositif symétrique par rapport à un plan perpendiculaire au plan de figure contenant l'axe (X'X), la conservation du flux magnétique conduit à :
Bn.Sn=BeSe=2Bb.Sb
Si l'entrefer est de longueur "Le" très petite devant les autres dimensions du dispositif : Sn=Se.
Si, de plus : Sn=2Sb, on arrive, comme tu l'as écrit dans ton premier message à :
Bn=Be=Bb.
Le théorème d'Ampère appliqué à un des deux contours fermés et orientés dessinés ci-dessous conduit à :
Hn.Ln+He.Le+Hb.L=N.I
Le champ d'induction magnétique étant sensiblement de même intensité en tout point du milieu ferromagnétique, on peut considérer µr comme constant dans ce milieu. Ce qui conduit à :
L désigne la longueur de la ligne de champ moyenne que j'ai dessinée à laquelle il faut soustraire (Ln+Le)
Merci !
Je ne savais pas que de chaque côté on avait Bb. Yaurait il une analogie à faire ?
Dans l'expression du théorème d'ampère, il ne manquerait pas le ?
Oui : terme de droite : µo.N.I . Étourderie de ma part... Désolé !
J'ai fait l'hypothèse (peut-être fausse : je n'ai pas d'énoncé complet) d'un cadre magnétique admettant un plan de symétrie comme déjà indiqué. Cela suppose que la section droite du "bord" droit et celle du "bord" gauche sont égales. Puisque les flux magnétiques sont égaux....
D'accord merci, donc si on l'écrit en flux, cela peut s'écrire :
En fait ce que j'ai encore du mal, je sais que de chaque côté l'induction est la même (symétrique), mais pourquoi on pourrait pas écrire au lieu de Bb de chaque côté Bb/2 car le flux est divisé par deux ?
Le flux est divisé par deux mais l'aire S de la section droite est aussi divisée par deux. Conséquence : Bn=Bb.
D'accord,
Pour finir est ce que il y a une vrai utilité d'avoir un entrefer dans le circuit magnétique ?
Avec des valeurs importantes du produit NI, on peut obtenir dans l'entrefer, donc dans l'air des champs magnétiques relativement intense.Placer des cet entrefer divers dispositifs permet d'étudier leurs comportements dans des champ magnétiques intenses.