J'ai oublié le schéma

Bonsoir
Ton raisonnement me semble correct. Dans le cas des deux diodes passantes, tu obtiens de façon plus directe s(t) par le théorème de Millman, histoire de vérifier que la méthode demandée conduit bien au même résultat.
Je vérifierai pas à pas tes calculs demain...

J'obtiens bien le même résultat pour s(t) avec Millman.
D'accord, merci

Comme déjà dit hier soir, la méthode utilisée me semble bonne mais, peut-être à cause de maladresses dans l'écriture des équations en ligne, je ne suis pas d'accord avec toutes tes équations. Je préfère reprendre brièvement.

Premier cas : D1 et D2 bloquées. D'accord avec toi : cela suppose : e(t)<E1 et alors :

s(t) = e(t)

Puisque E2>E1, nous avons aussi : e(t)<E2...

Deuxième cas : D1 passante et D2 bloquée. Le théorème de Millman conduit à :



D2 bloquée suppose : s(t)<E2 ; soit :



Le cas D1 passante et D2 bloquée suppose donc au final :



Troisième cas : les deux diodes sont passantes. Cela suppose que e(t) appartienne au domaine de valeurs restant soit :



Le théorème de Millman conduit simplement à :



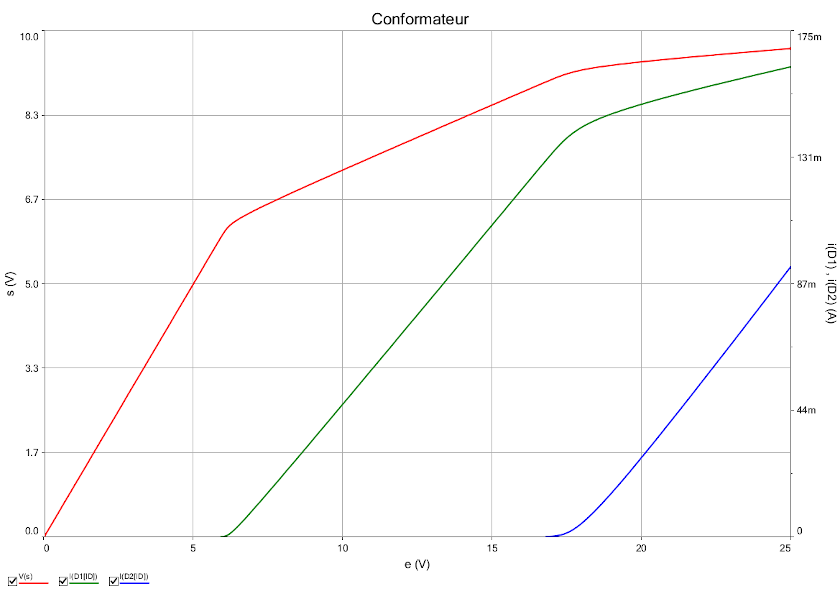
Pour illustrer tout cela, voici une simulation faite avec : R=60 ; R1=20 ; R2=3 ; E1=6V ; E2=9V.

Tu obtiens en rouge la courbe s(t)=f(e) ; en vert la courbe i(D1)=g(e) et en bleu la courbe i(D2)=h(e). La transformation Thévenin - Norton ne te pose pas de problème ; je n'en parle pas.

Merci beaucoup pour votre aide.
Avec vos explications, j'ai bien compris mes erreurs qui n'avaient parfois pas trop de sens ...

Je vais donc continuer avec la partie 2 :
Étude du conformateur à diodes

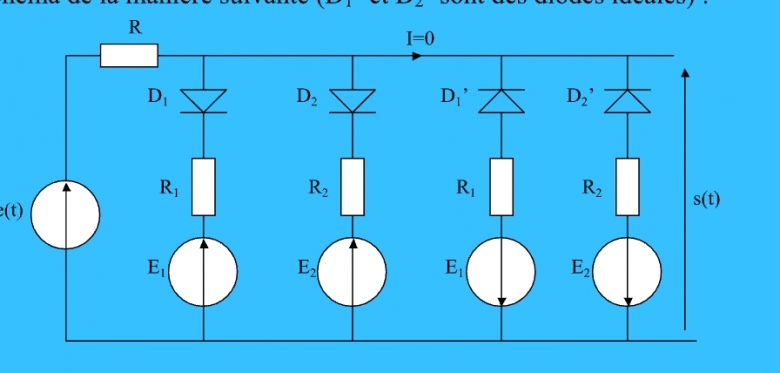
Afin de rendre impaire la caractéristique de transfert s(e) déterminée précédemment, nous pouvons transformer le schéma de la manière suivante (D1' et D2' diodes idéales) .

A)Dessiner la nouvelle caractéristiques de transfert s(e)

B) le signal d'entrée e(t) est un signal triangulaire de valeur moyenne nulle, de pulsation w et dont la valeur maximale E est supérieur aux valeurs des seuils déterminés au 1a
Tracer l'allure de la tension de sortie s(t) en fonction du temps.

C) On veut que le signal s(t) se rapproche le plus possible d'un signal sinusoïdal s(t) = Sm sin(wt) avec Sm = 6V. Pour cela on désire fixer le premier seuil à la valeur Sm sin (wT / 12) et le deuxième à la valeur Sm sin (wT /6 ). Enfin on désire que s(T/4) = Sm.
En déduire les valeurs des tensions E, E1 et E2
Calculer les résistances R1 et R2. On choisira R= 20 ohm.

J'ai beaucoup plus de mal avec cette partie ...
J'ai sais pas trop commencer, il faut sans doute réutiliser Millman pour la A

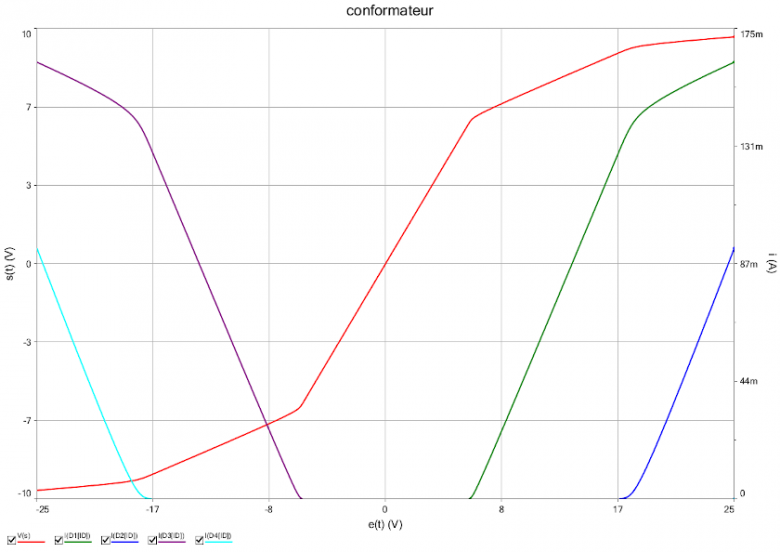
Rassure-toi : l'essentiel du travail a été fait à la partie 1. Il suffit maintenant de réfléchir un peu aux symétries. Pour t'aider un peu, je reprends la simulation précédente, sans modifier les valeurs numériques choisies un peu au hasard en faisant varier e(t) entre -e_max et e^max alors que précédemment, la variation se faisait de zéro à e_max=25V. Tu peux remarquer que, puisque la tension e(t) est alternative triangulaire, sur cette demie période, e(t) est proportionnel à t. Donc, à un facteur d'échelle près, l'axe horizontal peut être considéré comme l'axe des temps.
Pour e(t) compris entre zéro et e_max, D'1 et D'2 sont nécessairement bloquées. Le circuit se comporte donc comme celui de la partie 1.
Pour e(t) compris entre -e_max et zéro, D1 et D2 sont nécessairement bloquées. Tout se passe comme si leurs branches étaient supprimées du circuit. Par simétrie, on remarque alors que remplacer e(t) par -e(t) remplace s(t) par -s(t). Là encore : aucun calcul à faire !
Reste pour terminer à faire les applications numériques pour que la courbe rouge ressemble un peu plus à une demie période de sinusoïde avec s_max= 6V et non 9,5V comme sur la simulation.

Merci beaucoup, j'ai maintenant plutôt bien compris

Je trouve donc
1er seuil = sm sin 2pi/ 12 = E1 = 3V
2eme seuil = sm sin 2pi /6 = E2 = 5,2V

Avec l'équation du 3eme cas Millman on peut trouver Emax avec s(T/4) = sm
On trouve donc Emax = e(T/4) ... Mais il faut pour cela R1 et R2 ...

Je n'arrive pas à trouver ces 2 valeurs de résistances
J'ai essayé de chercher avec les continuités mais sans succès

D'accord pour E1 et E2.
Puisque e(t) correspond à une tension triangulaire, pendant le premier quart de période, sachant que e(0) = 0 et e(T/4)=E, on peut écrire, pendant ce premier quart de période :



Or : donc E ???

Il faut ensuite raisonner sur t=T/6 :

; Certaine relation fournie dans mon message du 01-03-21 à 15:42 va te permettre d'obtenir R1.

Pour obtenir R2, tu peux raisonner sur la date t=T/4 ; s et e sont connues à cette date. L'application du théorème de Millman (dernière relation du message du 01-03-21 à 15:42) permettent d'obtenir R2.
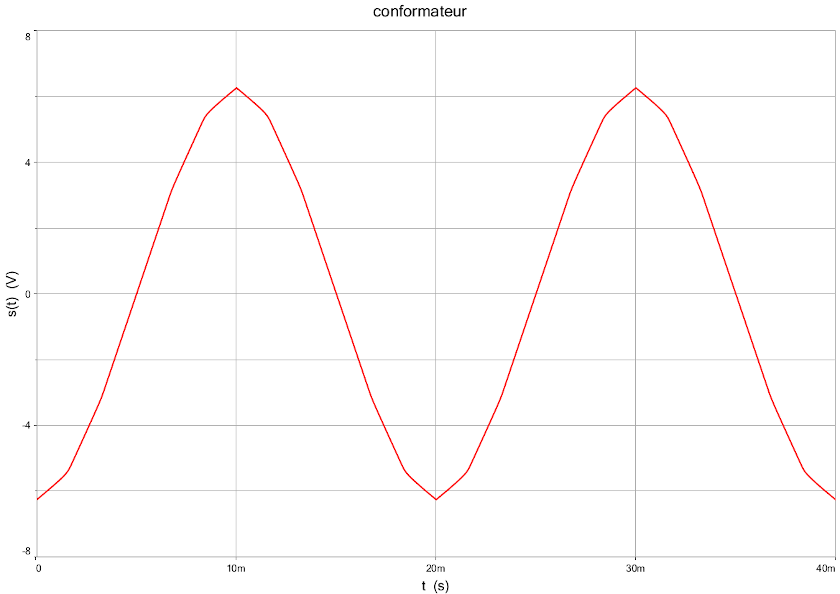
Voici le résultat obtenu pour s(t). J'ai choisi arbitrairement T=20ms. Ce n'est bien sûr pas tout à fait une sinusoïde mais le résultat est tout de même assez bon comme pourrait le montrer une analyse de Fourrier... On pourrait améliorer le montage en ajoutant quelques diodes supplémentaire pour obtenir un découpage en davantage de segments...

Ah oui ! J'avais pas du tout pensé à utiliser la forme de e(t) ...
Je trouve E = 9 V
R1 = 55 ohm
R2 = 8,4 ohm

Merci encore une fois pour ces aides et ces explications très intéressantes

Bonne soirée !

D'accord avec tes résultats !