Inscription / Connexion Nouveau Sujet
Conduite coudée
Bonsoir.
Je fais un exercice avec un Venturi, une tuyère et un coude, et je ne suis pas sûr de ce que j'ai fait à la fin de l'exercice. J'ai pris un référentiel (x,y) avec x vers la droite sur le schéma et y vers le haut.
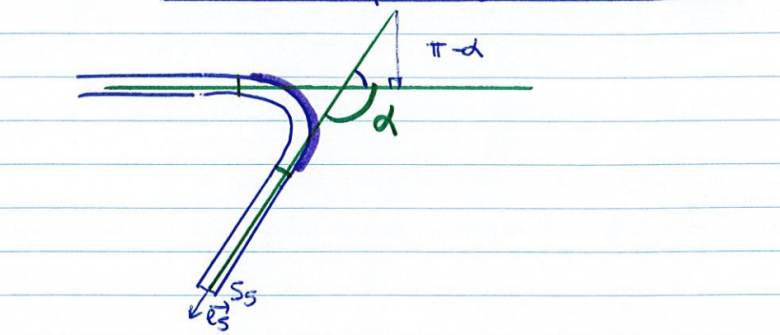
À l'entrée, il y a une vitesse v4 orientée selon l'axe x positif et en sortie une vitesse v4 orientée selon le vecteur (e5).
L'angle  est égal à 120°.
est égal à 120°.
Voici les questions (je traite les deux ensemble par la suite) :
1) Donner l'expression de la force exercée par le coude sur le jet et celle du jet sur le coude.
2) Calculer les composantes Fx et Fy de la force totale appliquée sur le coude. Justifiez pourquoi on a pas à prendre en compte la pression atmosphérique. Calculer la norme de la force du jet sur le coude et la valeur de l'angle de son orientation par rapport à l'axe x.
Voici ce que j'ai fait, à partir du bilan du flux de la quantité de mouvement :
.
Là c'est pour les justifications de ce que je vais dire que je ne suis pas sûr.
Pour le poids, je dirais qu'on a pas à le prendre en compte pour des raisons de symétrie et pour les forces de pression, je dirais qu'elles sont nulles car on est à pression atmosphérique à l'entrée et à la sortie du tube (est-ce que il y a une manière plus "mathématique" de le montrer ?).
Du coup l'expression de la force serait :
sa norme serait et la valeur de l'angle de son orientation par rapport à l'axe x, je ne sais pas trop.
Bonjour
N'ayant pas l'énoncé en entier, je ne vais pas nécessairement être d'une aide très efficace. Quelques remarques tout de même :
Ton expression de la force n'est pas homogène : une intensité de force peut s'écrire comme le produit d'un débit massique par une variation de vitesse...
Pour le reste, si je comprends bien l'énoncé : la pression en aval du coude et la pression en amont du coude sont toutes deux égales à la pression atmosphérique. Le théorème de Bernoulli montre facilement que la pression atmosphérique est dans de telles conditions sans influence sur la vitesse.
La déviation du jet par le coude se fait dans un plan horizontal ou un plan vertical ? Dans le second cas, il faut considérer que la variation d'énergie potentielle massique de pesanteur est d'influence négligeable.
Bonjour,
Merci pour ces remarques!
Ton expression de la force n'est pas homogène
J'ai oublié de mettre la surface en recopiant! Du coup ce serait
Voici l'énoncé complet :
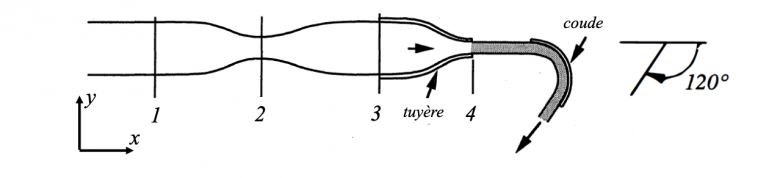
De l'eau s'écoule unidirectionnellement suivant Ox, de façon permanente, dans une conduite horizontale de symétrie cylindrique, qui comprend :
— une section cylindrique de rayon R1 = 0.1 m (section 1)
— un Venturi de diamètre au col R2 = 0.05 m (section 2)
— une tuyère convergente de rayon initial R3 = 0.1 m (section 3) et final R4 = 0.025 m (section 4, de sortie du jet dans l'atmosphère, où la pression est p0 = 10^5 Pa).
La tuyère est vissée sur la conduite et le jet qui s'échappe frappe un coude dont la coupe dans le plan horizontal xOy a la forme d'un arc de cercle. Le coude dévie l'écoulement de 120° de sa direction initiale. L' écoulement reste toujours dans le plan horizontal.
Le débit volumique est constant Qv = 0.2 m3/s. La masse volumique de l'eau est
On suppose que le fluide est incompressible et non visqueux.
Mais du coup pour le poids, ce serait parce qu'on est dans un plan horizontal et donc à même hauteur qu'il n'est pas pris en compte? Je n'arrive pas bien à visualiser la situation.
Dans le second cas, il faut considérer que la variation d'énergie potentielle massique de pesanteur est d'influence négligeable.
Nous sommes manifestement dans cette situation compte tenu de la valeur assez élevée du carré de la vitesse de l'eau.