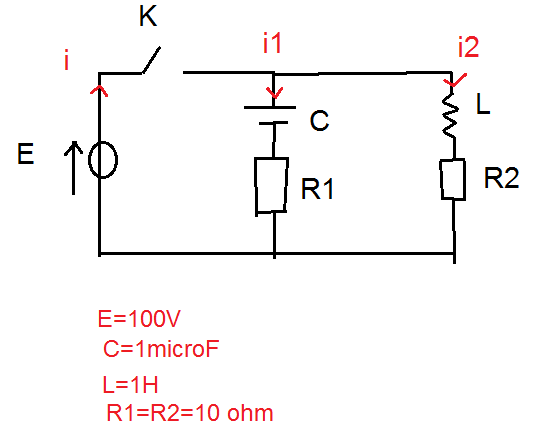
Oui, mais si le circuit est dans l'état du dessin (interrupteur ouvert) depuis suffisamment longtemps avant le fermeture de K, on a alors obligatoirement Uo = 0.

en réalité, le condensateur est branché en parallèle avec un générateur de tension Uo (avec un interrupteur K' fermé )

et t=0 correspond à l'instant on l'on ferme l'interrupteur K et on ouvre K'

Avec ce complément d'info, c'est bon... du moins si Uo est dans le "bon sens".

Merci et soit u(t) la tension aux bornes de C et R (ouL et R )

u(0)=E/R mais pour du/dt(0) je coince..

Si tu veux avoir des réponses cohérentes, écris l'entièreté de lénoncé, sans y changer un mot... et avec aussi un schama complet.

En fait nous avons montré précédemment qu'on avait l'equa diff suivante pour le circuit :

di^2/dt^2 +2/di/dt +1/^2 i = 1/R(du^2/dt^2 +2/du/dt +1/^2 u

où =RC=L/R , de plus on a démontré que R1=R2

3) déterminer i(0) et di/dt(0) 4)trouver l'ED générale pour i(t) 5)donner une solution particulière 6)donner l'expression totale de i

3) i(0)=(E-Uo)/R et di/dt(0)=E/L -(E-Uo)/R^2C  

4) i(t)SG= exp(-t/)(At+B)

5) u(t)/R est solution particulière

6) i(t)= exp(-t/)(At+B) + u(t)/R  

je trouve B=(E-Uo)/R  pour A je bloque et en fait , je suis sensé trouver une solution qui ressemble à celle d'une equa diff du 1er ordre..  

Merci d'avance

Comme quoi, certains aiment se compliquer la vie ...

i = i1 + i2

E = R1.i1 + Uc
avec i1 = C.dUc/dt

R1.di1/dt + i1/C = 0
i1 = A.e^(-t/(R1.C))
i1(0) = (E-Vo)/R (puisque C était chargé en t = 0)
i1 = ((E-Vo)/R).e^(-t/(R1.C))
---
E = L.di2/dt + R2.i2

i2 = B.e^((-R2/L).t) + E/R2
i2(0) = Uo/(R1+R2) ... toujours en supposant Uo imposé (depuis longtemps) sur C en t = 0-

Uo/(R1+R2) = B + E/R2
B = Uo/(R1+R2) - E/R2
i2 = (Uo/(R1+R2) - E/R2).e^((-R2/L).t) + E/R2
---

i = i1 + i2

i(t) = ((E-Uo)/R).e^(-t/(R1.C)) + (Uo/(R1+R2) - E/R2).e^((-R2/L).t) + E/R2

Mais toujours sans avoir l'énoncé original et le dessin original de l'énoncé ...

Et donc sujet à de mauvaises interprétations.
-----
Sauf distraction.  

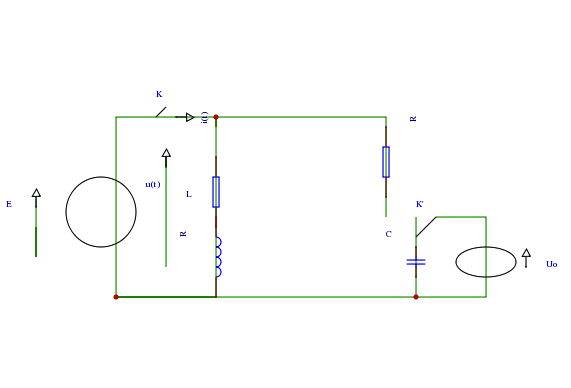
Rebonjour.  et merci pour votre réponse. Voici le vrai schéma.

J'ai donné l'énoncé comme tel, le seul soucis, c'est que nous sommes sensé une solution pour i(t) qui ressemble à une solution d'une Equa diff du premier ordre.. à cause de la disposition du circuit et des relations liant les composants  

De plus, à t<0 , K est ouvert et K' positionné comme sur le schéma , à t>0 , on inverse.

...

Et évidemment, différent de ce qui pouvait être imaginé.

...
i2 = B.e^((-R2/L).t) + E/R2
i2(0) = 0
i2 = E/R2 * (1 - e^((-R2/L).t))

i = i1 + i2

i(t) = ((E-Vo)/R).e^(-t/(R1.C)) + (E/R2) * (1 - e^((-R2/L).t))

Sauf distraction.  

Merci beaucoup pour tout