Inscription / Connexion Nouveau Sujet
Conditions de stabilité d'une échelle inclinée
 leprof001
leprof001Bonjour,
Voici un sujet :
Une échelle M de longueur h est appuyée en A contre un mur lisse.
En B (sur le sol) l'angle d'adhérence est de 15°. L'échelle sur laquelle est montée un homme est inclinée par rapport au sol de 60°.
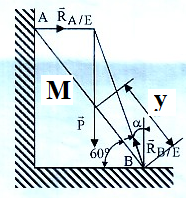
Travail à faire
Trouver la condition de stabilité de cette échelle en considérant que le poids de l'échelle est de 5 N
Merci d'avance pour vos réponses
bonsoir,
l'échelle est stable s'il n'y a pas glissement en B donc si  < 15° ou encore tg
< 15° ou encore tg  < tg 15°
< tg 15°
tu peux trouver tg  graphiquement
graphiquement
(ou en calculant RB avec les lois de la statique, mais c'est plus lourd)
Mais les lois de la statique me donnent :R(A/E)-R(B/E)sin(alpha)=0 et -p1(de l'homme)-p2(de l'échelle)+R(B/E)cos(alpha)=0 j'en déduit que R(B/E)=(p1+p2)/cos(alpha) et donc R(A/E)=(P1+p2)*tg(alpha).
Le moment est ce qu'on le calcule par rapport à A ou B ?
Supposons qu'on le calcule par rapport à B, on aura :
-R(A/E)*l*sin(60) +(p1+p2)*y*sin(30)=0 or sin(60)=cos(30) et y=l/2 on en déduit donc que R(A/E)=(1/2)*(p1+p2)*tg(30)
J'espère que je ne me trompe pas.
on a donc tg(alpha)=(1/2)*tg(30) or tg(30)=1/(racine(3)) alors tg(alpha)=1/(2racine(3)) et alpha=16.10° (je pensas que alpha devrait être égal à 15° est ce cette réponse de 16.10° est juste ?
merci de continuer avec moi la discussion
En appelant P1 le poids de l'échelle (supposé appliqué au milieu de l'échelle) et P2 le poids du bonhomme supposé monté sur l'échelle (de longueur L) au point repéré par le y.
Somme des moments des forces par rapport à B = 0 (tant que l'échelle ne glisse pas)
Avec angle en B = 60°, on a :
P1.L/4 + P2.y/2 = (Ra.L.V3)/2
RA = (P1.L + 2P2.y)/(2V3.L)
La composante verticale de la réaction du sol en B est |P1+P2| vers la haut
La composante horizontale de la réaction du sol en B est |Ra| (vers la gauche)
On a donc tg(alpha) = RA/(P1+P2) = (P1.L + 2P2.y)/[2V3.L.(P1+P2)]
Pour ne pas glisser, il faut donc que : (P1.L + 2P2.y)/[2V3.L.(P1+P2)] <= tg(15°)
-----
Exemple numérique :
P1 = 5 N (Vérifie cela, cette valeur est loufoque).
Supposons P2 = 800 N
Supposons L = 3 m
(5*3 + 2*800.y)/[2V3*3*805] < 0,268
15 + 1600y < 2243
y < 1,39 m
Si le bonhomme monte plus haut que y = 1,39 m, bardaf ...
-----
Toutes erreurs incluses (rien relu). 


