Inscription / Connexion Nouveau Sujet
condensateur sphérique
bonjour j'ai une petit problème pour les question2, 3,5,6 ,4 ... je ne vois pas comment attaquer le problème .
voici l'énoncé :
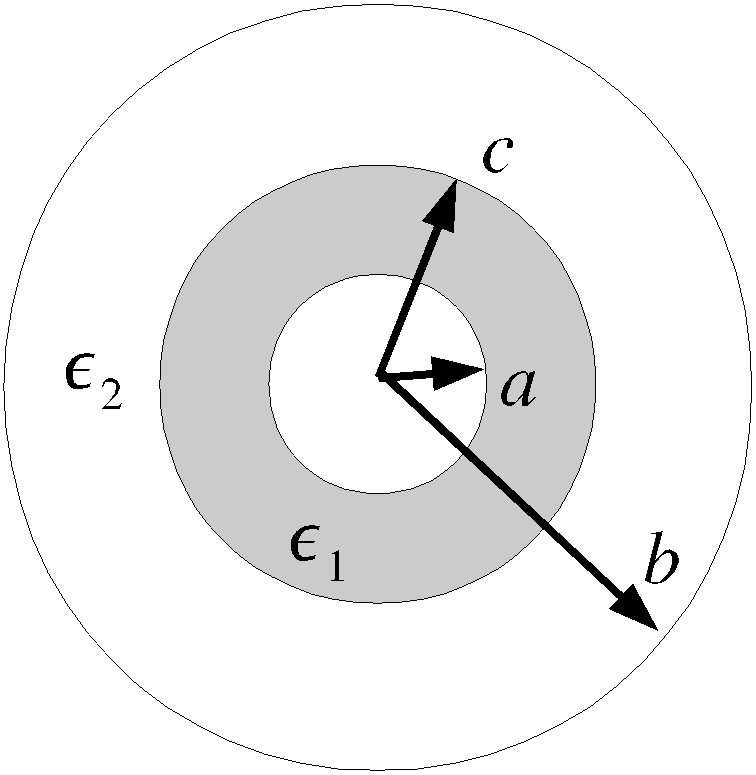
On considere un condensateur spherique dont le rayon des armatures vaut respectivement a et b .
• Determiner la capacite C0 de ce condensateur lorsque le vide separe les armatures.
• Meme question lorsqu'un dielectrique de permittivite relative (espilon r ) est introduit entre les deux arma tures. Soit Cr cette nouvelle capacite.
Maintenant, l'espace compris entre les armatures est rempli de deux dielectriques tels que:
epsilon = epsilon 0 epsilon 1 pour a ≤ r < c
epsilon = epsilon 0 epsilon 2 pour c ≤ r < b
2/ déterminer D et E dans les milieux . en déduire la différence de potentiel Va-Vb
et la capacité C d'un tel condensateur .
debut de réponse
D1=epsi o epsilon1*E1
D2=epsio epsi1*E2
3/montrer que c verifie la relation :
1/C=1/C1 +1/C2 interpreter les coefficients c1 et c2 .
4/ • Quelles sont les densites de charge de polarisation sur la surface de rayon a du dielectrique, sur l'interface de rayon c commun aux deux dielectriques et sur la surface de rayon b du dielectrique.
5/• Quelle est la densit´e de charge volumique de polarisation.
6/• Faire le bilan des charges de polarisation
Bonsoir
Suggestion :
commence par étudier attentivement l'énoncé du 4ème fichier (Exam.SN2013-2014.pdf) et le corrigé correspondant, le 9ième fichier (Solution Exam.SN2013-2014.pdf) que tu trouveras ici :
![]()
Ils correspondent à quelques détails près à ton exercice. Si le corrigé ne te parait pas clair, n'hésite pas à demander des éclaircissements sur ce forum.
j'ai bien essayer de comprendre votre correction mais je n'arrive pas a faire le lien avec mon problème ...
Bonsoir
Juste quelques indications pour les questions 2 et suivantes. Il faut considérer une charge Q répartie uniformément sur la sphère de rayon a et une charge (-Q) répartie uniformément sur la sphère de rayon b.
1° L'étude des plans de symétries et des invariances montre que les vecteurs champs E et D sont radiaux ; leurs composantes non nulles ainsi que le potentiel ne dépendent que de r.
2° L'équation différentielle locale : permet d'appliquer au vecteur D le théorème de Gauss en choisissant comme surface de Gauss une sphère de centre O et de rayon r quelconque :
3° Les milieux étant homogènes, linéaires et isotropes, on déduit facilement les expressions de E en fonction de celle de D.
4° En régime permanent : ; on déduit les expressions du potentiel des expressions de E . Sachant que la source du champ est d'extension finie, on peut choisir le potentiel arbitrairement nul à l'infini.
5° En déduire l'expression de la capacité.
La suite est une application directe du cours.
bonjour,
je crois avoir compris :
pour arc je trouve E1=Q/4a20
ensuite je deduis D1= 0
0  1 E1 =Q1/4
1 E1 =Q1/4 a a
a a
et de meme pour D2 =-Q2/4bbet E2=-Q/4bb  0
0
puis pour les capacites :
 (de a a c ) E1.ds +
(de a a c ) E1.ds + (de c a b) E2 .ds =
(de c a b) E2 .ds =  ( de 0 a b )Etot .ds
( de 0 a b )Etot .ds
et je suppose qu'on trouve 1/C0=1/C1+1/C2
je n'ai pas fait le calcul encore mais je remettrai un message pour confirmer les valeurs
je remarque que c'est le meme principe que des résistance en dérivation 1/Rtot = sur i des 1/Ri
sur i des 1/Ri
ici on a
1/Ctot = i des 1/Ci
i des 1/Ci
. Si vous pouviez me donner votre opinion se serait trés aimable de votre part merci !
Bonjour
Si vous pouviez me donner votre opinion se serait trés aimable de votre part merci
Ce n'est pas vraiment cela : D,E et V dépende de r : la distance au centre du condensateur. Quand tu écris :
j'ai bien essayer de comprendre votre correction mais je n'arrive pas a faire le lien avec mon problème
Je me demande si tu n'as fait la confusion entre le fichier SN2013.2014.pdf (le quatrième de la liste) et le fichier SR2013.2014.pdf (le premier de la liste) ? Le fichier "SR..." est très différent de ton étude. En revanche, le fichier "SN..." a de nombreux points communs avec ton étude.
Je te laisse réfléchir... Suggestion : commence par étudier et comprendre l'exercice proposé sur le site ; tu verras ensuite que la résolution de ton exercice te paraîtra facile...
As-tu compris les indications fournies dans mon message précédent du 25-06-17 à 01:40 ?
je retente
pour 0 r<a
r<a
D=0 et E=0
pour a r<c
r<c
D1=Q/4 r2
r2  0
0  1
1
D1= 0
0  1 E1
1 E1
d'ou E1= Q/4 r2 (
r2 ( 0
0  1)2
1)2
pour c r<b
r<b
D2= 0
0  2 E2
2 E2
E2=- Q/4 r2 (
r2 ( 0
0  2)2
2)2
ensuite pour la capacité total du condensateur on calcul les circulations
V1-V2 =a  b E1 .dl =Q/4
b E1 .dl =Q/4
 0
0  1 a
1 a cr-2 dr - c
cr-2 dr - c bQ/4
bQ/4
 0
0  2
2
r-2dr
V1-V2 = Q /4
 0 (1/
0 (1/ 1 ((c-a)/ac +1/
1 ((c-a)/ac +1/  2 ((b-c)/bc))
2 ((b-c)/bc))
C= 4
 0 / (1/
0 / (1/ 1 ((c-a)/ac +1/
1 ((c-a)/ac +1/  2 ((b-c)/bc))
2 ((b-c)/bc))
finalement on a en prenant l'inverse de l'expression on obtient bien
1/C = 1/C1 +1/C2
voila et cela ressemble etrangement au resistance en derivation
1/Rtotal =i
 1/Ri
1/Ri
donc pour un condensateur avec plusieur dielectriques on aura
1/C total =i
 1/Ci
1/Ci
je planche sur les autres questions maintenant merci de me confirmer les resultats s'il vous plait .
pour la polarisation
 =-div(P)
=-div(P)
 =P.n
=P.n
P=( -
- 0)E1 =(
0)E1 =( r1-1)/
r1-1)/ r1 ) Q/4
r1 ) Q/4 r^2
r^2
ensuite je ne comprends pas trop comment faire ...
Tu es en progrès mais attention : le théorème de Gauss appliqué au vecteur D fait intervenir les charges réelles et la géométrie de la source de champ mais pas le milieu matériel où on étudie le champ. Comme déjà écrit tout à l'heure :
Cela conduit à :
dans les isolants et un vecteur nul ailleurs.
Je te laisse corriger le reste en conséquence.
donc dans les 2 milieux dielectrique pour a<r<c et c<r<b on a bien D = Q/ 4 r2 et pour r<a et r>b D= O
r2 et pour r<a et r>b D= O
c'est ce que j'ai fait il me semble non ?
Relis ton message du 25-06-17 à 17:17 : tu fais bien intervenir les permittivités dans les expressions de D !
Pour ton message de 17h29 , il te faut calculer la divergence du vecteur E. Si tu ne connais pas l'expression de la divergence d'un vecteur en coordonnées sphériques, tu la trouveras ici : (dernière page du document operateurs.pdf) :
![]()
donc je reprend des le debut :
je trouve D1=Q/4 r2
r2
E1= 1/ 0
0 1(Q/4
1(Q/4 r2)
r2)
puis D2= -Q/4 r2
r2
E2= 1/ 0
0 1(Q/4
1(Q/4 r2)
r2)
puis l'intégrale reste la même que précedemment dans le message de 17h17
je trouve bien 1/c=1/c1+1/c2
voila mon erreur etait seulement sur les vecteurs D n'est ce pas ?
ensuite pour la divergence de E :
E=E(r)
d'ou div(E) = 1/r2  (r 2e(r))/
(r 2e(r))/ r
r
aprés je ne vois pas comment continuer pour trouver les charges de polarisations sur la surface de rayon a de rayon c et de rayon b ? si vous pouviez m'indiquer un chemin se serait trés aimable .
Tu as déjà écrit ce qu'il faut faire !
Question 5 : Le calcul précédent va te permettre de montrer que la divergence du vecteur P est nulle dans les isolants : densité volumique de charge de polarisation nulle en tout point des isolants.
Question 4 : En revanche, sur les sphères de centre O et de rayons a,b et c, les composantes normales du vecteur P ne sont pas nulles : tu vas devoir définir des densités surfaciques de charges de polarisation non nulles.
Question 6 : évidente j'espère.
question 5:
donc dans le milieu 1
div (E1) = 1/r2 ( 2r3 Q/4
 -2r3Q/4
-2r3Q/4
 )=0 !
)=0 !
Div (E2) = 0 aussi
div (E  0)=
0)= -div(P)
-div(P)
-div (P)= dans les deux milieux
dans les deux milieux

.gif) / n(a,b,c)
/ n(a,b,c)
