Inscription / Connexion Nouveau Sujet
Accueil l'île de la physique - chimie Forum de physique - chimieListe de tous les forums de physique - chimie SupérieurOn parle exclusivement de physique/chimie, pour le supérieur principalement, les BTS, IUT, prépas... LicenceForum Supérieur de licence PhysiqueTopics traitant de Physique [tout]Lister tous les topics de physique - chimie
Niveau licence
Partager :

Compressibilité isotherme

Posté par
Farogenious 30-01-22 à 00:16

Bonjour, Bonsoir,

Je suis étudiant en Biologie, Chimie, et dans la matière mécanique des fluides on a un exercice qui m'embête un peu... Je n'ai pas un niveau formidable en maths et je suis en train de m'instruire sur les dérivées partielles mais avec encore beaucoup de lacune.  Je viens donc vous voir pour que vous puissiez m'aider à comprendre l'énoncé et à m'éclairer sur l'utilité de la dérivé partielle dans ce cas et de sa résolution, je me tiendrais à disposition pour faire marcher mes méninges et essayer de le résoudre moi-même avec votre aide.

Du coup l'énoncé est :

Le facteur de compressibilité isotherme X_{T} est définie par :

X_{T} = -\frac{1}{V}(\frac{\partial V}{\partial P})_{T}

1) Exprimer X_{T} en fonction de la masse volumique \rho et de ses dérivées.

Ma réponse partielle...

Tout d'abord si j'ai bien compris la dérivée partielle ici sert à nous dire qu'on veut étudié pour une variation infinitésimale de P de combien varie V à température constante. Ensuite je ne sais pas pourquoi on divise par \frac{-1}{V} (pas beaucoup de description sur le net...)

Ensuite je suppose que si je veux exprimer la masse volumique en fonction de la compressibilité isotherme je dois trouver une relation que je peux placer dans l'équation :

D'où :

\rho = \frac{m}{V} \Leftrightarrow V = m.\rho

Donc :

X_{T} = -\frac{1}{V}(\frac{\partial V}{\partial P})_{T}, avec  V = m.\rho
Alors :

X_{T} = -\frac{1}{V}(\frac{\partial (m.\rho)}{\partial P})_{T}

et là je suis bloqué en supposant que ce que j'ai trouvé est juste mais bon je crois pas trop...

Merci d'avance pour vos réponses.

Posté par
vanoisere : Compressibilité isotherme 30-01-22 à 11:22

Bonjour
Tu es sur la bonne voie. Il suffit de remplacer V par son expression en fonction de m et de sachant que l'on travaille sur un système fermé donc un système de masse constante.

Posté par
Farogeniousre : Compressibilité isotherme 30-01-22 à 11:40

Bonjour Vanoise et merci pour ta réponse. Cela me rassure mais je débute en thermodynamique. Si je comprends bien un système fermé correspond à un échange d'énergie (Travail en l'occurrence) mais pas de matière.

Dans ce cas comment savoir que notre système est de nature fermé ? Je peux sans doute imaginer le cas d'un piston, quand la pression augmente, le volume diminue sous l'action d'une force, et la compressibilité me renseigne sur la fraction du volume compressé en fonction de la variation de la pression, si j'ai bien compris. Dans ce cas il y aurait un échange d'énergie sous forme de travail.

Autre point si comme vous me le dites nous somme dans un système fermée et que la masse est constante je peut donc sortir la masse de la dérivé partielle.  Ce qui donne :

X_{T} = -\frac{1}{V}(\frac{\partial (m.\rho)}{\partial P}), avec  \Delta m = 0

\Leftrightarrow -\frac{m}{V}(\frac{\partial (\rho)}{\partial P})

Et ensuite je me lance dans la résolution mais je ne comprends pas : " en fonction de ses dérivées"

Cela m'aide déjà beaucoup Merci !

Posté par
Farogeniousre : Compressibilité isotherme 30-01-22 à 12:49

Du coup je me lance dans la résolution de X_{T} en fonction de \rho :

On sait que :

X_{T} = -\frac{1}{V} (\frac{\partial V}{\partial P})_{T}

Le système est de nature fermé donc : m = cte

\rho  est définie par :   \rho = \frac{m}{V}

Résolution, peut être pas juste mais pas grave

X_{T} = -\frac{1}{V} (\frac{\partial V}{\partial P})_{T}, avec V = m.\rho

\Leftrightarrow -\frac{1}{V} (\frac{\partial (m.\rho)}{\partial P})_{T} sachant que le système et fermé donc \Delta m = 0   (cte)

\Leftrightarrow -\frac{m}{V} (\frac{\partial (\rho)}{\partial P})_{T}

Or je dois dériver par rapport à \partial P donc il faut que je trouve le moyen de faire sortir P à partir de \rho .

Dans le cas d'un gaz parfait on a :

P.V = n.R.T

Sachant que \rho = \frac{m}{V} alors on à :

\Leftrightarrow V = \frac{n.R.T}{P} soit :

\rho = \frac{m}{V}

\Leftrightarrow \frac{m}{\frac{n.R.T}{P}}

\Leftrightarrow \frac{m.P}{n.R.T}

Ce qui revient a écrire :

X_{T} = -\frac{m}{V} (\frac{\partial \rho}{\partial P})_{T}

\Leftrightarrow -\frac{m}{V} (\frac{\partial (\frac{m.P}{n.R.T})}{\partial P})_{T}

Sachant que la masse "m", la quantité de matière "n", la constante des gaz parfait "R", et la Température "T" sont considéré comme constant.


Soit :

X_{T} = -\frac{m}{V} (\frac{\partial (C.P)}{\partial P})_{T}, avec   C =\frac{m}{n.R.T}

Résolution de la dérivée partielle :

     Règle sur les dérivées : si f(x) = ax    alors     f'(x) = a

Donc :

X_{T} = -\frac{m}{V}.C

On remplace C et on obtient :

X_{T} = -\frac{m}{V}.\frac{m}{n.R.T} = -\frac{m^{2}}{n.R.T.V} = - \rho \frac{m}{n.R.T}    car  \rho = \frac{m}{V}

\Leftrightarrow -\rho. M_{mol}\frac{1}{R.T},  (  car    M = \frac{m}{n}  )   = -\frac{\rho.M_{mol}}{R.T}


Donc en fonction de la masse volumique on a (si tout est bon) :

X_{T} = -\frac{\rho.M_{mol}}{R.T}

Posté par
vanoisere : Compressibilité isotherme 30-01-22 à 12:57

Citation :
Si je comprends bien un système fermé correspond à un échange d'énergie (Travail en l'occurrence) mais pas de matière.

Dans ce cas comment savoir que notre système est de nature fermé ?

Cela a sans doute été précisé par ton professeur dans son premier cours de thermo et depuis, cela est systématiquement sous-entendu. En effet, l'étude des systèmes ouverts est traitée en général beaucoup plus tard dans le programme (au niveau bac+2 en général) et d'ailleurs pas nécessairement dans ta filière. Comme tu l'as écrit, un système fermé n'échange pas de matière mais peut échanger du travail et aussi de la chaleur.
La masse volumique est le quotient m/V et non l'inverse.

\chi_{T}=-\dfrac{\rho}{m}\cdot\left(\dfrac{\partial\left(\frac{m}{\rho}\right)}{\partial P}\right)_{T}
Je te laisse terminer le calcul.

Posté par
Farogeniousre : Compressibilité isotherme 30-01-22 à 13:38

Merci autant pour moi une erreur bête pour la masse volumique, je me relance, et je chercherais dans mon cours de Thermodynamique.

En espérant que la prochaine démonstration soit la bonne

Posté par
Farogeniousre : Compressibilité isotherme 30-01-22 à 15:54

Me revoilà pour une nouvelle démonstration (Juste, espérons le) :

On considère :

\huge X_{T} = -\frac{1}{V}\left(\frac{\partial V}{\partial P}\right)_{T}


comme étant la compressibilité isotherme, et le système comme étant fermé (aucun échange de matière).

On nous demande alors d'exprimer  \large X_{T}   en fonction de la masse volumique  \large \rho    


Soit :

\large \rho = \frac{m}{V}     \Leftrightarrow     V = \frac{m}{\rho}



\large \emph{On représente} :   X_{T}   \emph{en fonction de}   \rho :

\large \large X_{T} = -\frac{1}{\frac{m}{\rho}}(\frac{\partial (\frac{m}{\rho})}{\partial P})_{T} \Leftrightarrow -\frac{\rho}{m} (\frac{\partial(\frac{m}{\rho} )}{\partial P})



\large \emph{Sachant que le système est fermé alors :}  \Delta m = \emph{cte}, \emph{ce qui donne :}

\large X_{T} = -\rho (\frac{\partial(\frac{1}{\rho} )}{\partial P})


\large \emph{Pour calculer la dérivée partielle : } \frac{\partial (\frac{1}{\rho})}{\partial P}, \emph{il faut exprmier P en fonction de }\rho, \emph{ ce qui donne :}

\large Avec : \rho = \frac{m}{V}

\large et

\large P.V= n.R.T \Leftrightarrow V = \frac{n.R.T}{P}

\large alors :

\large \rho = \frac{m.P}{n.R.T}




\large \emph{On considère que m, n, R et T sont constant, on peut donc dire que :}

\large \rho = \frac{m.P}{n.R.T} \Leftrightarrow \rho = \frac{m}{n.R.T} . P


\large \emph{On émet l'égalité suivante: } \rho = \alpha . P \emph{ avec } \alpha = \frac{m}{n.R.T}

\large \emph{Donc : }

\large \rho = \alpha.P


\large \emph{On aurait alors :}

\huge X_{T} = -\rho \left(\frac{\partial\left(\frac{1}{\alpha.P} \right)}{\partial P}\right)_{T}




\large \emph{On résout la dérivée partielle}

\huge \frac{\partial\left(\frac{1}{\alpha.P} \right)}{\partial P},\; f\left(P \right) = \frac{1}{\alpha.P} \rightarrow f'\left(P \right) = \frac{-\alpha}{(\alpha . P)^2} \Leftrightarrow -\frac{1}{\alpha . P^2}


\large \emph{On a donc :}

\huge X_{T} = -\rho . \left(-\frac{1}{\alpha . P^2} \right)



\large \emph{On oublie pas de remplacer par } \alpha :


\huge X_{T} = -\rho . \left(-\frac{1}{\alpha . P^2} \right) \Leftrightarrow \frac{\rho}{\alpha . P^2} \Leftrightarrow \frac{1}{\alpha} \frac{\rho}{P^2} \Leftrightarrow \frac{n.R.T}{m} \frac{\rho}{P^2}, \emph{avec } \alpha = \frac{n.R.T}{m}

\huge X_{T} = \frac{n.R.T.\rho}{m.P^2}


Il nous est possible de simplifier :


\huge \emph{Sachant que } V= \frac{n.R.T}{P}, \; et \; \rho = \frac{m}{V}, \; alors :


\huge \frac{n.R.T.\rho}{m.P^2} = \frac{V.\rho}{m.P} = \frac{V.m}{m.V.P} = \frac{1}{P}


\huge \emph{Donc :}

\huge X_{T} = \frac{1}{P}


j'espère que cette fois ci c'est la bonne sinon je recommencerez tant pis

Posté par
Farogeniousre : Compressibilité isotherme 30-01-22 à 16:13

Pardon petite coquille :

\huge \alpha = \frac{m}{nRT}

Posté par
vanoisere : Compressibilité isotherme 30-01-22 à 19:08

Tel que je lis l'énoncé que tu as recopié, il s'agit d'exprimer 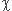T en fonction de et de dérivées partielles de et rien ne précise que le système est un gaz parfait. Je me contenterais donc personnellement de la réponse suivante, mais bon : je n'ai pas sous les yeux l'énoncé complet...
Puisque m est une constante, on peut sortir m de la dérivée :

\chi_{T}=-\frac{\rho}{m}\cdot\left(\frac{\partial\left(\frac{m}{\rho}\right)}{\partial P}\right)_{T}=-\rho\cdot\left(\frac{\partial\left(\frac{1}{\rho}\right)}{\partial P}\right)_{T}

Cours de math :

\left(\frac{\partial\left(\frac{1}{\rho}\right)}{\partial P}\right)_{T}=-\frac{1}{\rho^{2}}\cdot\left(\frac{\partial\rho}{\partial P}\right)_{T}

Donc :

\chi_{T}=\frac{1}{\rho}\cdot\left(\frac{\partial\rho}{\partial P}\right)_{T}

A noter une formulation analogue de celle fournie par l'énoncé avec cependant un changement de signe ; puisque le coefficient de compressibilité isotherme est positif, une augmentation isotherme de pression d'un système fermé et homogène diminue son volume et augmente sa masse volumique.

Posté par
Farogeniousre : Compressibilité isotherme 31-01-22 à 09:42

Alors oui l'énoncé n'est pas très bien rédigé mais j'utilise le contexte d'un gaz parfait, car ensuite il nous demande de calculer le facteur de compressibilité isotherme d'un gaz parfait, et pour finir on nous propose de résoudre un problème. J'essaye de faire tout ça et je créerais un nouveau sujet. je garde la notation dans le cadre d'un non-gaz parfait qui peut être intéressant et utilisable dans différents cas j'imagine.  

En tout cas Grand Merci j'ai pu apprendre en maths et physique grâce à votre aide, à bientôt


Rechercher
Menu
Espace membre
Changer d'île
Mentions légales - Retrouvez cette page sur l'île de la physique - chimie
© digiSchool 2025

Vous devez être membre accéder à ce service...

Pas encore inscrit ?

1 compte par personne, multi-compte interdit !

Ou identifiez-vous :

Rester sur la page

Désolé, votre version d'Internet Explorer est plus que périmée ! Merci de le mettre à jour ou de télécharger Firefox ou Google Chrome pour utiliser le site. Votre ordinateur vous remerciera !