Inscription / Connexion Nouveau Sujet
Comportement d'une bobine
Bonsoir.
Je m'interroge sur un point concernant un circuit électrique :
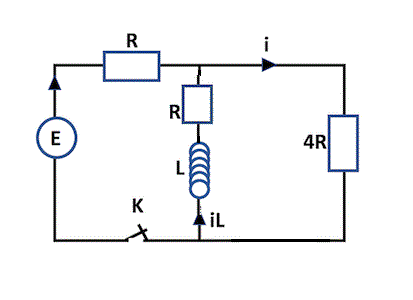
On a deux mailles, sur la branche la plus à gauche, un générateur de tension E qui impose un courant "vers le haut", suivi une résistance R puis dans la branche du milieu, une bobine L dont le courant iL va vers elle et en haut de la bobine, une résistance R. Enfin, dans la branche la plus à droite, une résistance 4R qui reçoit un courant i. Notons la présence d'un interrupteur k ouvert situé sur le fil faisant la jonction entre la branche de gauche et la branche du milieu.
(J'espère que c'est clair, je n'arrive malheureusement pas à joindre de schéma.)
Bref, tout ça pour dire que :
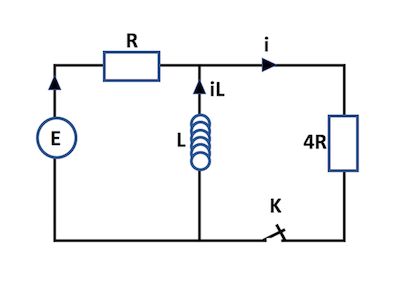
- lorsque l'on ferme l'interrupteur resté ouvert pendant un certain temps, le courant aux bornes de la bobine est continu et nul (on enlève la branche contenant la bobine)
- quand on atteint le régime permanent (t tend vers l'infini) alors la bobine est comme un fil
- et quand on ouvre de nouveau l'interrupteur ? Que se passe-t-il ? C'est ce point là que je n'arrive pas à éclaircir. Comment simplifier le schéma compte-tenu de cette situation ?
Merci par avance pour vos explications !
Hello
1) Histoire de regarder dans la même direction. C'est cela ton circuit?
2) Si oui, peux tu décrire qualitativement ce qui se passe jusqu'au moment où l'on ouvre à nouveau l'interrupteur K?
@J-P: J'ai toujours confondu ma droite et ma gauche, quant au centre je le cherche toujours ... Merci!
On y est presque ^^
Parfait pour la maille de droite mais à gauche (@J-P) la résistance est "au-dessus" de E et l'interrupteur est à la place du R (qui est au-dessus de E comme je viens de le dire).
On y est presque ^^
Parfait pour la maille de droite mais à gauche (@J-P) la résistance est "au-dessus" de E et l'interrupteur est à la place du R (qui est au-dessus de E comme je viens de le dire).
C'est électriquement strictement équivalent.
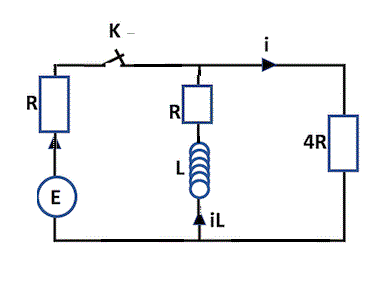

A comprendre ... avant d'essayer d'établir i(t) pour t > 0 dans le dessin de droite.
Sauf distraction 
Donc d'après ton schéma de droite, lorsque K s'ouvre, il n'y a plus de courant dans la maille de gauche. Comment se fait-il en fait que... ce soit la bobine qui impose le courant ?
Question subsidiaire sur ton schéma de gauche : comment établit-on les valeurs d'intensité avec K fermé ? J'imagine que l'on raisonne séparément en enlevant la branche de la bobine d'une part, et en mettant un fil en régime permanent d'autre part (après équation différentielle) ?
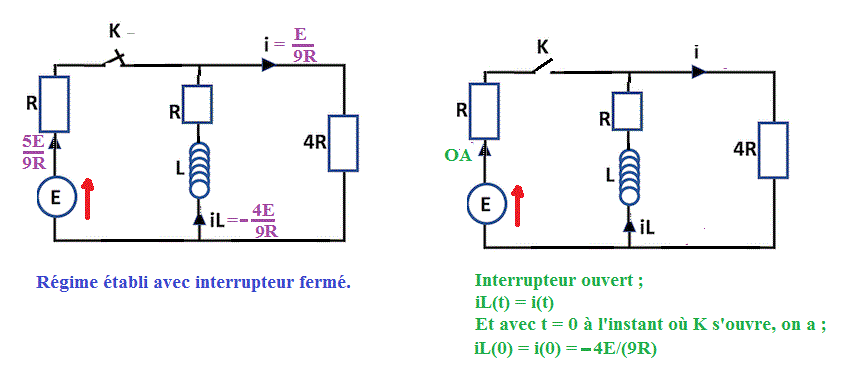
Je viens de réaliser que je ne parviens pas à trouver les 5E/9R etc.
Peux-tu me donner ta démarche ?
"Comment se fait-il en fait que... ce soit la bobine qui impose le courant ?"
Il ne peut pas y avoir de discontinuité (saut brusque) de l'intensité de courant dans une bobine... et donc l'intensité dans la bobine est la même en t = 0- qu'en t = 0+ (donc juste à l'instant précédant l'ouverture de K et l'instant suivant l'ouverture de K)
---------------
"Comment établit-on les valeurs d'intensité avec K fermé"
En régime établi, l'inductance se comporte comme un court-circuit ... et donc la générateur de tension E est chargé par une impédance Z = R en série avec (R en parallèle sur 4R)
Z = R + 1/(1/R + 1/(4R))
Z = R + (4/5)R = 9R/5
Le courant "sortant" du générateur est donc égal à E/Z = E/(9R/5) = 5E/(9R)
...
Sauf distraction.

Merci pour ta réponse - et le temps que tu prends pour m'expliquer.
Le souci, c'est que mon prof' ne m'a jamais parlé ni d'impédance ni d'inductance qui se comporte comme un court-circuit.
Si tu as quelques explications, je suis preneuse !
Bien sûr qu'on t'en a parlé, peut être avec d'autres mots (qu'il faut comprendre)
Tu as écris le même chose avec ta phrase : "quand on atteint le régime permanent (t tend vers l'infini) alors la bobine est comme un fil "
Un simple fil est équivalent à un court-circuit.

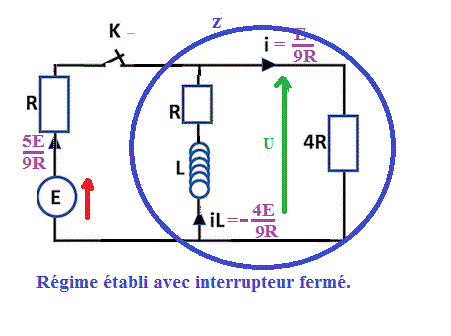
Soit par calcul ... soit par un raisonnement simple.
Quand on a trouvé le courant dans le générateur (5E/(9R))
Ce courant se "coupe" en deux branches, l'une d'imésdance R (puisque nen régime établi, L à une umpédance nulle) et l'autre d'impédance 4R
Donc le courant dans la branche d'impédance R et 4 fois fois celui de la branche à impédance 4 R
Donc 1/5 de (5E/(9R)) = E/(9R) passe dans la branche d'impédance 4R
et 4/5 de (5E/(9R)) = 4E/(9R) passe dans la branche d'impédance R ... mais compte tenu du sens des flèche sur le courant, on a iL = -4E/(9R)
-----
Par calcul :
L'impédance de la branche R+L et celle de 4 R est en régime établi : z = R//4R = 4R²/(5R) = (4/5) * R
Donc la tension U aux bornes de cette impédance esr U = z * i génerateur = (4/5) * R * 5E/(9R) = (4/9).E
Et on a : U = 4R * i --> i = U/(4R) = E/(9R)
et on a aussi : U = -R.iL --> IL = - U/R = -(4/9).E/R
Sauf distraction. 
Merci de prendre tout ce temps pour m'aider !
Pourquoi a-t-on le droit de calculer une telle résistance équivalente z=4/5*R ?
En régime établi, le "z" que j'ai entouré en bleu sur mon dessin est équivalent à une résistance R en parallèle sur une résistance 4 R (car L se comporte comme un court-circuit en régime établi), et donc :
1/z = 1/R + 1/(4R) (calcul pour des résistances en //)
1/z = 4/(4R) + 1/(4R)
1/z = 5/(4R)
z = 4R/5