Niveau maths sup

Comportement d'une automobile

Posté par
Kai22 22-02-17 à 22:05

Bonsoir.

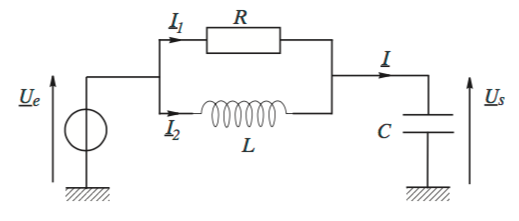
Voilà un bon moment que je bloque sur un exercice, dont je joins le schéma de la situation.
Il s'agit d'un circuit électrique et on me demande la puissance MOYENNE dissipée par la résistance.

Dans un premier temps, j'ai calculer l'impédance complexe équivalente de l'intégralité du circuit :
$\bar{Z}=\frac{R-RCLw^2+jLw}{jCw(R+jLw)}$ ce qui est bien conforme à la correction

Mais je ne m'en sors pas avec la puissance. En étudiant le corrigé, j'ai :
$P=\frac{1}{2}RI_1^2$ ce que je comprends bien.
Ensuite : $P=\frac{1}{2}\frac{U_R^2}{R}$ ce qui va encore.
MAIS c'est là que je décroche :
$P=\frac{1}{2R}\frac{L^2w^2}{1+\frac{L^2w^2}{R^2}}I^2$
Que vaut explicitement U_R ?

De même, ça se complique avec :
$P=\frac{1}{2R}\frac{L^2w^2}{1+\frac{L^2w^2}{R^2}}I^2[tex]\frac{C^2w^2(1+\frac{L^2w^2}{R^2})}{(1-LCw^2)^2+\frac{L^2w^2}{R^2}}U_e^2$
[/tex]

J'ai l'impression que la "grosse fraction" est une impédance mais à quoi correspond-elle ?

Un grand merci par avance pour vos explications

$Comportement d\'une automobile$

Posté par re : Comportement d'une automobile 23-02-17 à 00:04

Bonsoir
Je crois que tu t'es trompé de titre...
Je note $\underline{Ze}$ l'impédance équivalente à l'association en parallèle de R et de L :

$\underline{Ze}=\frac{jLR\omega}{R+jL\omega}$
L'ensemble Ze en série avec C constitue un diviseur de tension, la tension commune aux bornes de R et de L (orientation récepteur : flèche de la tension orientée en sens inverse de la flèche orientant I1) est ainsi :

$\underline{U_{R}}=\underline{U_{e}}\cdot\frac{\underline{Z_{e}}}{\underline{Z_{e}}+\frac{1}{jC\omega}}=\underline{U_{e}}\cdot\frac{\frac{jLR\omega}{R+jL\omega}}{\frac{jLR\omega}{R+jL\omega}+\frac{1}{jC\omega}}=\underline{U_{e}}\cdot\frac{jLR\omega}{jLR\omega+\frac{R+jL\omega}{jC\omega}}$

$\underline{U_{R}}=\underline{U_{e}}\cdot\frac{-RLC\omega^{2}}{R+jL\omega-RLC\omega^{2}} \\$
La puissance moyenne consommée par R s'écrit :

$P=\frac{1}{2}\frac{U_{R}^{2}}{R}$
où Ur désigne la valeur maximale de la tension aux bornes de R soit le module de $\underline{U_{R}}$ . Or, tu as sûrement vu en math que le carré du module d'un complexe est le produit du complexe par le conjugué de celui-ci. Pour obtenir le conjugué d'un complexe, il suffit de remplacer j par (-j) dans son expression. Cela donne, en notant Ue la valeur maximale de Ue (attention : pas sa valeur efficace !) :

$P=\frac{U_{e}^{2}}{2R}\cdot\frac{-RLC\omega^{2}}{R+jL\omega-RLC\omega^{2}}\cdot\frac{-RLC\omega^{2}}{R-jL\omega-RLC\omega^{2}}$

$P=\frac{U_{e}^{2}}{2R}\cdot\frac{\left(RLC\omega^{2}\right)^{2}}{\left(R-RLC\omega^{2}\right)^{2}+\left(L\omega\right)^{2}}$
Sachant que la valeur efficace de la tension d'entrée est : $U_{eff}=\frac{U_{e}}{\sqrt{2}}$ , l'expression de la puissance moyenne consommée par R peut aussi s'écrire :

$P=\frac{U_{eff}^{2}}{R}\cdot\frac{\left(LC\omega^{2}\right)^{2}}{\left(1-LC\omega^{2}\right)^{2}+\left(\frac{L\omega}{R}\right)^{2}}$

On peut vérifier l'homogénéité de la formule puisque $LC\omega^{2}$ et $\frac{L\omega}{R}$ sont sans dimension physique. On peut aussi vérifier les cas limites :

Cas limite $\omega\rightarrow0$ ; la bobine se comporte comme un simple fil de résistance négligeable qui court-circuite la résistance et, de plus, le condensateur se comporte comme un interrupteur ouvert. Aucun courant ne traverse la résistance. Dans l'expression précédente, on vérifie facilement que $P\rightarrow0$ dans ce cas.

Cas limite $\omega\rightarrow\infty$ ; la bobine se comporte alors comme une impédance infinie parcourue par aucun courant, tout se passe comme si elle n'existait pas. L'impédance du condensateur tend vers zéro, celui-ci se comporte comme un fil de résistance nulle. Tout se passe comme si le générateur de tension Ue alimentait uniquement R. On vérifie mathématiquement :

$\lim_{\omega\rightarrow\infty}\left(P\right)=\frac{U_{eff}^{2}}{R}$

Évidemment, ces vérifications permettent de détecter de grossières erreurs mais ne permettent pas d'éviter toutes les fautes de calculs et il se fait tard...
Remarque : la formule qui te fais décrocher est sans doute la formule du diviseur de courant... Il m'a paru plus simple de passer par celle du diviseur de tension en général mieux connue des étudiants...