Inscription / Connexion Nouveau Sujet
Comment calculer le torseur d'un solide animé par trois forces
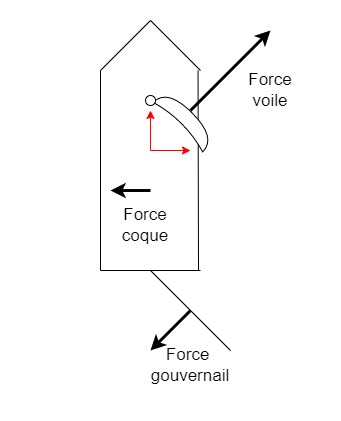
Bonjour à tous. J'essaie de modéliser les forces agissant sur un voilier pour un petit jeu vidéo.
Si on ramène le problème à un plan (vu de dessus) nous avons trois forces : voile, coque et gouvernail. Ces forces provoquent une rotation et une force résultante au voilier. Ces forces sont en déséquilibre. Comment trouver le centre de rotation instantané du bateau, l'intensité du moment au centre de rotation et la force résultante ?
Merci beaucoup pour votre aide !
Bonjour,
Il faut deja bien definir le (ou les repères) pour pouvoir parametrer la position du solide.
On peut ensuite ecrire les lois du mouvement en G, centre de masse, pour determiner les accelerations (si on connait les forces) et enfin integrer tout ca (en se donnant des conditions i nitiales) pour trouver la position de G et la rotation du solide autour de G.
Ici, on ne sait rien du champ de vitesses , ca va etre dur de trouver d'emblée le C.I.R.
Bonjour Krinn,
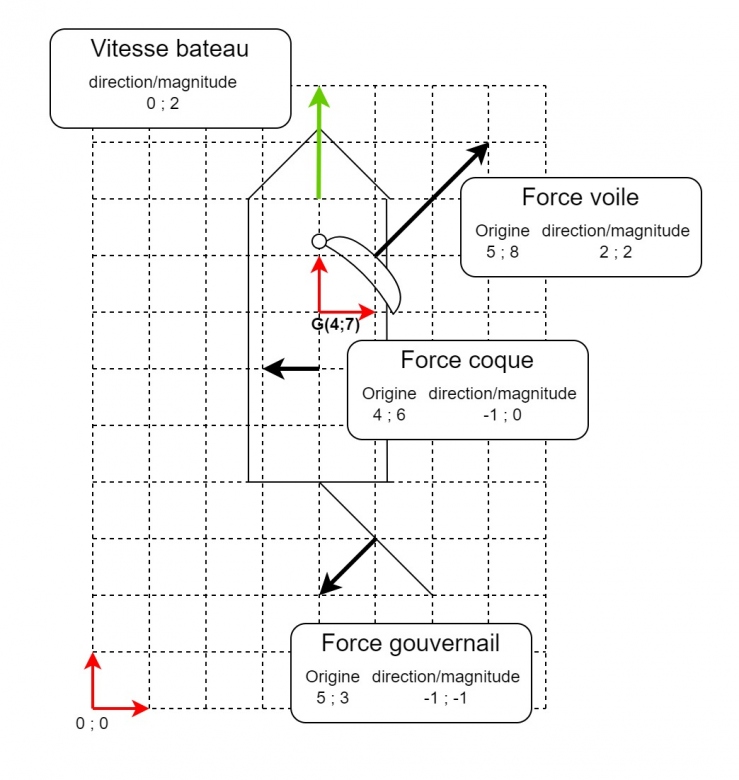
Merci beaucoup pour ton aide. J'ai complété le problème en définissant les forces qui agissent sur le bateau (points d'applications, directions et magnitudes), avec une vitesse du bateau en plus. J'ai écrit les lois du mouvement au niveau du centre de gravité G et je trouve une résultante de direction/magnitude (0 ; 1). Tu dis qu'il faut ensuite intégrer tout ça pour trouver le centre de rotation. Comment procéder ? Voici un nouveau schémas avec plus de données.
Bonsoir,
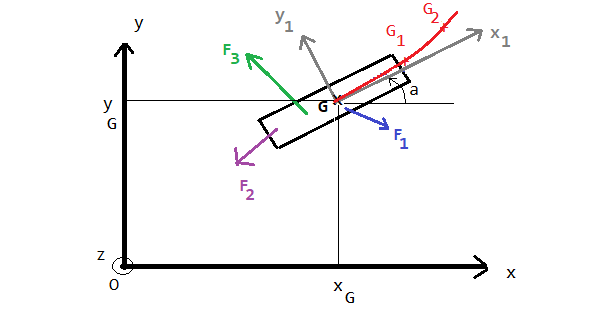
Je propose un repérage un peu plus précis (cf. figure).
Il faut en effet repérer non seulement G mais l'orientation du solide avec l'angle  entre (O,x) et (G,x1)
entre (O,x) et (G,x1)
Ensuite, on écrit la 2e loi de Newton pour trouver x" et y" à l'instant t=to (puisque les forces sont connus) et on en déduit la vitesse et puis la position à l'instant t + t (avec
t (avec  t = 1s par ex.) , en faisant une approximation, au 1ere ordre par ex. :
t = 1s par ex.) , en faisant une approximation, au 1ere ordre par ex. :
x'(t+ t)
t)  x'(t) + x"(t)
x'(t) + x"(t)  t
t
y'(t+ t)
t)  y'(t) + y"(t)
y'(t) + y"(t)  t
t
puis
x(t+ t)
t)  x(t) + x'(t)
x(t) + x'(t)  t
t
y(t+ t)
t)  y(t) + y'(t)
y(t) + y'(t)  t
t
Il reste à déterminer la nouvelle orientation ( ) à t+
) à t+ t, soit avec la mécanique du solide, soit par une autre approche.
t, soit avec la mécanique du solide, soit par une autre approche.
Et à recalculer la projection des forces dans (O,x,y) en fct des nouvelles coordonnées (x,y,x',y', ), le cas échéant.
), le cas échéant.
Puis tu répètes l'opération (en partant de t+ t ) pour trouver ainsi pas à pas le mvt (approché) en 2D.
t ) pour trouver ainsi pas à pas le mvt (approché) en 2D.
Note qu'il y a des méthodes plus précises pour évaluer x'(t) et x(t) mais pour l'instant on en reste au principe.
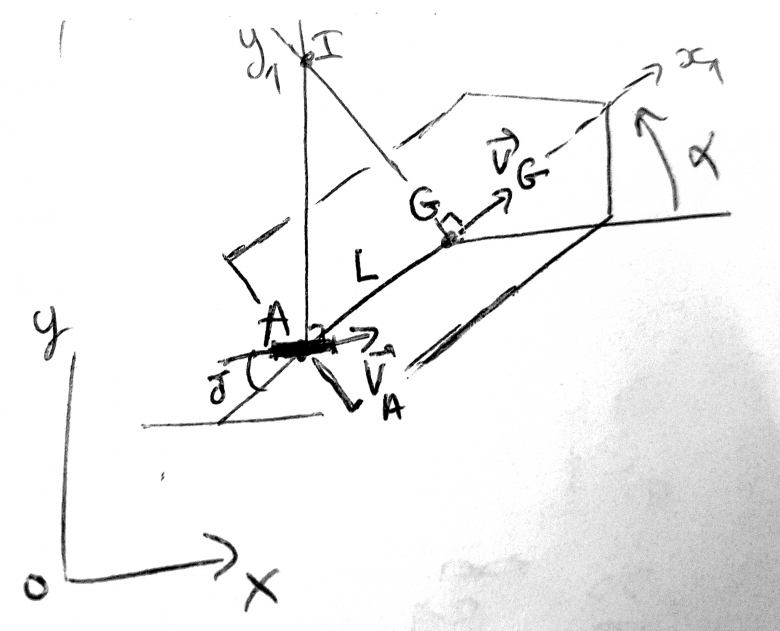
En fait on peut simplifier enormement le modèle et alors determiner le C.I.R. comme tu le souhaites , cf figure:
notations:
G: centre de masse
A: barre
 : angle de barre
: angle de barre
I: C.I.R
(x,y, ): position du solide
): position du solide
(x',y') : composantes de  G
G
v : valeur de  G
G
on trouve alors un modele tres simple (par tres realiste) :
x'=v cos
y'=v sin 
 =
=  ' = v tg
' = v tg /L
/L
On n'a donc plus que v comme variable.
Et la 2e moi de Newton nous donne en proj. sur (G,x1) la dynamique du systeme :
m dv/dt = ....
Ca se rapproche plus du mvt d'un tricycle que de celui dun voilier 
Mais c'est tres simple.
Note: on dirait qu'il manque une force de trainee dans ton modele, du type f=-kv opposée à  G
G
Merci beaucoup pour ta réponse. Ton approche de l'avant-dernière réponse est très bien pour être implémentée en code et pour ajouter des forces supplémentaires. En effet il manque à mon modèle la trainée, merci beaucoup pour la remarque. J'ai commencé à coder le modèle. Chaque force a son petit modèle mathématique qui tourne à la première étape du calcul pour ensuite appliquer ta méthode. Pour trouver la nouvelle orientation Alpha à t+1, quelle méthode utiliserais tu ? J'ai songé à calculer la somme des moments de toutes les forces au niveau d'un point arbitraires (le point G par exemple). Initialement je pensais trouver un point de l'espace où la somme des moments soit nulle, mais je trouve une droite où la somme des moments est nulle en tous points (droite qui a le même sens que la résultante des forces). Le point où appliquer les moments peut-il être arbitraire ? Est-ce que je peux lier le moment à une accélération angulaire de la même façon que je peux lier une force à un accélération ?
Bonsoir,
Graphiquement ca part pas mal...
ici le problème étant plan on n'a qu'une équation régissant la rotation et le plus simple est de se placer en G :
Jz  " =
" =  moments / G
moments / G
où Jz est le moment d'inertie du bateau par rapport à (G,z)
Tu trouveras au début de ce document un modèle de voilier qui a l'air assez simple (et qui a donné apparemment de bon résultats) : -> ![]()
Bonjour Krinn !
Merci beaucoup pour ce document. Il est incroyablement inspirant. Je pourrai réutiliser le modèle en ajoutant des forces supplémentaires. Fondamentalement elles sont toutes ramenées au centre de gravité G pour s'exprimer. Il n'y aurait donc pas de limites à leur nombre. C'est un projet très enrichissant. Encore merci pour l'aide que tu m'as apporté.
De rien.
Je pourrai réutiliser le modèle en ajoutant des forces supplémentaires.
Fondamentalement elles sont toutes ramenées au centre de gravité G pour s'exprimer. Il n'y aurait donc pas de limites à leur nombre.
Attention quand meme car il faut que le schéma ait des solutions stables sinon le systeme risque davoir un comportement erratique, sans compter les soucis avec la resolution numerique!
Je te conseille de faire dabord un modele simple et d'essayer de bien voir les conditions de stabilité, notamment pour le cap.
On a ici un systeme forcement non lineaire, ca nest pas du tout evident....


