Inscription / Connexion Nouveau Sujet
Cohesion du chlorure de Sodium
Bonjour tous le monde !
J'ai un devoir à faire, et je ne sais pas trop comment démarrer...
Voici le sujet !
On considère le système représenté figure 1 : un ion Cl− est fixé à l'origine x = 0 et un ion Na+
de masse m est contraint à se déplacer sur l'axe des abscisses de vecteur unitaire i . La position de
Na+ est repérée par l'abscisse x(t). On suppose x(t = 0) > 0 et on montrera par la suite que
dans ce cas x(t) > 0 ∀t (ce qui correspond à l'impossibilité pour ces deux ions de
s'interpénétrer).
(i) etude du système Na+ - Cl-
1 - La force qui assure la cohésion du cristal est la force électromagnétique. Celle qui s'exerce sur
l'ion Na+ s'écrit:
Fel(x) = - A/x2 i
a) Montrer qu'il existe une énergie potentielle Eel(x) associée à cette force, déterminer son
expression en fonction de x. Où serait-il le plus judicieux de choisir l'origine des énergies
potentielles ?
b) Rappeler comment on appelle une force ainsi “associée” à une énergie potentielle et une
définition équivalente (en terme de travail) de cette catégorie de force.
2 - Pour garantir la non-interpénétration des ions, il existe des forces répulsives à courte distance
que l'on modélisera par leur énergie potentielle répulsive :
Erep(x) = B/x8
Calculer la force Frep(x) s'exerçant sur l'ion Na associée à cette énergie potentielle. Vérifier
que cette force est bien répulsive.
Mes pistes:
1-a) Lorsqu'il existe une Energie potentielle , elle est associée à F est conservative selon la definition
On a une fonction Ep(M) de la position de M telle que :
Wa->b(F) = Ep(A) - Ep(B)
On supposera que le chemin est rectiligne
dEp/dx = -F(x). i
Ep(x)= - intégrale de 0 à x F(s) . ids + C
il faudrait donc integrer l'expression?
Si on utilise l'origine du de EP, si Ep(x) est une energie potentielle alors Ep(x) + C ou C est une constante
Il faut donc trouver le point x pour lequel Ep(x) = 0
b) Une force qui est ainsi "associé" à une énergie potentielle est la force Conservative.
2 - Normalement si la force est bien repulsive alors on a une signe négatif au résultat .
Voila tous ce que j'ai comme commencement, j'espère que je suis sur la bonne voie
merci beaucoup !
Akkinda.
Bonsoir
Ce que tu as écrit sur le travail d'une force conservative est correct mais il est plus simple ici d'écrire
F = -(dEp/dx)
puis d'intégrer par rapport à x.
Fel(x) = -A/x2i
On a donc Eelp(x) = integrale allant de 0 à x( Fel(x) . i dx) = A * - 1/ x + C . i
Eel = - A / x + C . i
il faudra donc trouver C et voir si la méthode avec l'origine est plus efficace que de trouver s'il existe une energie potentielle.
Par convention, on choisit l'énergie potentielle nulle à l'infini. Cela permet d'obtenir la constante.
Ah D'accord, donc on a : Eel = - A/x
Est-il utile de trouver la variable A ?
Peut-on deja argumenter sur la méthode utilisé?
A doit être ici considérée comme une donnée du problème. Si tu as étudié par ailleurs la loi de Coulomb sur la force électrostatique d'attraction entre une charge positive et une charge négative, tu dois être capable d'exprimer A mais cela n'est pas demandé ici.
On obtient bien :
avec A : constante positive
Pour la question ou il faut argumenter, je pense que prendre l'integrale est plus judicieux que l'origine de l'energie, car tout dépend du point que l'ont prend ? Est-ce que c'est correcte ?
Raisonnement analogue à celui que tu as déjà fait pour l'énergie potentielle de pesanteur. Tu détermines l'énergie potentielle à une constante près par la méthode que je t'ai indiquée puis tu choisis arbitrairement un état d'énergie potentielle nulle : ici le cas limite où x tend vers l'infini.
Maintenant : libre à toi de suivre ou non mes conseils !
Je pense n'avoir pas très bien compris :
On prend un x pour lequel Ep(x) = 0
on refaite l'intégrale et on retrouve C qui est égale à 0?
Dans le cas le plus général d'un repère cartésien à trois dimensions, lorsqu'une force de vecteur est conservative, on peut lui associer une énergie potentielle que je note Ep (note la Up si tu préfères) telle que :
Si les trois composantes de la force sont connues, des intégrations permettent d'obtenir l'énergie potentielle à une constante arbitraire près. En effet : une primitive est toujours définie à une constante près. Dans le cas d'un problème à une dimension, cela donne :
Manifestement, tu « tournes en rond » alors que le résultat a été trouvé il y a longtemps. Je reprends une dernière fois :
Les primitives par rapport à x sont égales à une constante près :
On choisit la convention suivante :
donc :
donc :
J'aurais une autre question concernant ce même exercice.. :
3.d On suppose à présent que Na+ s'approche assez de Cl- (x<< 1) pour que la force electromagnétique de cohesion devienne négligeable devant la force de repulsion
Dans le cadre de cette approximaion, justifier l'hypothese afirmant que si x(t=0) > 0 alors, x(t)>0
determiner l'abscisse mnimum xmin > 0 ?
piste :
pour cette question comme dans les questions précédente nous avons trouvé Frep on sait que Fel est négligeable donc égale à 0.
qu'est-ce que vous en pensez ?
Il faut utiliser le raisonnement que je t'ai déjà indiqué en sens inverse. Puisque l'énergie potentielle associée à la force de répulsion est : Erep(x) = B/x8, tu obtiens la force associée par la relation :
Tu vas obtenir une force de répulsion orientée dans le sens positif. Puisque, à ces très courtes distances, la force électrostatique est négligée, l'ion va s'animer d'un mouvement dans le sens positif si l'abscisse initiale est positive et si la vitesse initiale est nulle (oubli de cette dernière condition dans ton énoncé).
Trouver l'abscisse minimale possible supposerait de connaître les conditions initiales. L'énoncé, tel que tu l'as copié, n'indique rien à ce sujet. Il s'agit peut-être de trouver la position d'équilibre stable. Elle correspond à un minimum de l'énergie potentielle totale : celle de répulsion et celle d'origine électrostatique.
Voici l'allure de la courbe représentant les variations de cette énergie potentielle totale en fonction de x (unités totalement arbitraires)
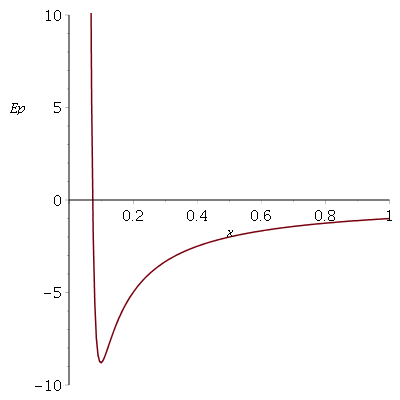
Bonjour,
J'ai fait : Em = Eel + Erep + Ec
On a x8min = 2B/V02 × m
Qui donne xmin =8 sqrt(2B/V02×m)
Est-ce que c'est bon
Et on nous demande de trouver xequilibre grace a la definition qnde la position equilibre ( un point materiel est a l'equilibre si la somme des forces appliquées est nulle)
Il faut trouver si il est instable ou stable grace a dEp/dx = - f(x) = - F(x).i
Une position d'equilibre x = xeq?
Si Vo désigne la vitesse à l'infini (ce qui n'a pas été précisé sur le forum), ton expression de xmin est correcte, à l'oubli près de parenthèses dans la formule.
Pour la position d'équilibre : l'explication détaillée a été fournie dans mon message du 10-12-19 à 12:21
v0 = 2 * 106
et xeq doit alors etre considéré comme stable comme on fait le raisonnement inverse il faut derivé l'expression
OK mais cela se simplifie ! Ensuite, pour la stabilité de l'équilibre, il suffit de montrer que cette position d'équilibre correspond à un minimum d'énergie potentielle.
Je trouve ainsi :
7squrt( 8B = (-A)) = xeq
Pour montrer que cette position d'equilibre correspond a un minimum
on remplace xeq par son expression ?
( Et si on avait dérivée Fel et Frep aurait-on eut le même résultat ?)
Ecrite ainsi, ta formule n'est pas claire et même incorrecte !
Pour savoir si x=xeq correspond à un maximum ou à un minimum d'énergie potentielle totale, il faut étudier les signes de la dérivée de l'énergie potentielle totale par rapport au temps et remplir un tableau de variations comme tu as appris à le faire en cours de math.
7sqrt( 8B/A) (C'est pas - A?)
Ep = Eel + Erep
<=> -A/x + B/x8
f'(x) = (-A+B) * -7/x8 et on fait le tableau de variation
x8 > 0
(-A+B)*-7 = 7A+-7B
(C'est pas - A?)
Il te faut vraiment commencer par revoir ton cours de math...
Revois aussi les calculs de dérivées...
Aah ok j'obtiens bien :
A/x2+ - 8B/x9
Quand j'entre ceci a la calculatrice je n'obtiens pas d'extrema est-ce normal ?
Ep fait intervenir un terme en 1/x8 qui devient très rapidement négligeable dès que x augmente. Pour bien mettre en évidence le minimum, il faut demander à la calculatrice un tracé pour des valeurs proches de x à l'équilibre.


