Niveau maths spé

Cohérence spatiale - trou d'Young

Posté par
iSirrol 08-01-16 à 20:28

Bonjour

$Cohérence spatiale - trou d\'Young$
J'ai établi la différentielle de l'intensité sous cette forme :
$\mathrm{d}I=\dfrac{I_0}{2}(1+\cos(2\pi\sigma(\frac{z}{D}+\frac{b}{d}))\mathrm{d}\textcolor{red}{?})$
je ne sais pas sur quoi intégrer pour arriver à un résultat de la forme :
$\mathcal{E}(z)=\dfrac{\mathcal{E}_0}{2}[1+\mathcal{V}\cos(\dfrac{2\pi z}{\epsilon})]$ avec $\epsilon$ l'interfrange qu'on devra exprimer $D$ , $a$ et $\sigma$

je connais la méthode mathématiques pour obtenir une visibilité en sinus cardinal, mais mon soucis est sur la variable d'intégration et les bornes à choisir, aiguillez moi sur ce point si vous voyez

j'aurai tendance à dire qu'il faut intégrer sur $b$ mais je ne sais pas pourquoi ni les bornes si c'est le cas

Posté par re : Cohérence spatiale - trou d'Young 09-01-16 à 00:04

Bonsoir,
Il s'agit bien d'étudier l'influence de la largeur b de la fente source sur la visibilité des franges ?
Un petit conseil préliminaire : essaie de ne pas mélanger intensité lumineuse et éclairement énergétique même si, dans ce contexte, ce sont deux grandeurs proportionnelles : choisi l'une ou l'autre mais pas les deux dans un même exercice.
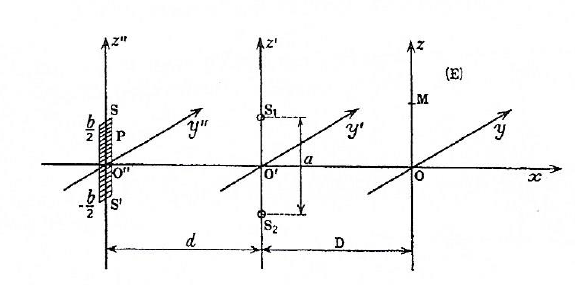
La méthode consiste à considérer la fente source comme une succession de fentes sources élémentaires incohérentes de largeur élémentaire dz". La fente source élémentaire de largeur dz", de cote z", produit sur l'écran d'observation un système de franges correspondant à un éclairement proportionnel à la largeur dz" de la fente source :

$\boxed{dE(z)=\frac{K}{2}\left[1+\cos\left[2\pi\sigma\left(\frac{z}{D}+\frac{z^{,,}}{d}\right)\right]\right]dz^{,,}}$
Les sources élémentaires étant incohérentes, les ondes qu'elles émettent n'interfèrent pas mais, la couleur étant la même, les éclairement énergétiques s'ajoutent.
Il te faut ensuite intégrer par rapport à z" de (-b/2) à (+b/2) à z fixe, pour obtenir l'expression de l'éclairement en fonction de z.

Posté par re : Cohérence spatiale - trou d'Young 10-01-16 à 14:24

vanoise @ 09-01-2016 à 00:04

Il s'agit bien d'étudier l'influence de la largeur b de la fente source sur la visibilité des franges ?

la question exacte est d'établir, l'éclairement sous cette forme :
$\mathcal{E}(z)=\dfrac{\mathcal{E}_0}{2}[1+\mathcal{V}\cos(\dfrac{2\pi z}{\epsilon})]$ avec $\epsilon$ l'interfrange qu'on devra exprimer $D$ , $a$ et $\sigma$

vanoise @ 09-01-2016 à 00:04

Un petit conseil préliminaire : essaie de ne pas mélanger intensité lumineuse et éclairement énergétique même si, dans ce contexte, ce sont deux grandeurs proportionnelles : choisi l'une ou l'autre mais pas les deux dans un même exercice.

Certes ce n'est pas pareil mais la seule formule de Fresnel qu'on ait est celle portant sur l'intensité et on me demande d'obtenir un résultat en éclairement. Mais comme c'est proportionnel ça ne change pas le raisonnement.

vanoise @ 09-01-2016 à 00:04

Il te faut ensuite intégrer par rapport à z" de (-b/2) à (+b/2) à z fixe, pour obtenir l'expression de l'éclairement en fonction de z.

merci c'est tout à fait ça que je voulais savoir, en fait j'ai calculer le déphasage en prenant $b$ comme la variable alors qu'il fallait prendre $z''$ , je vois mieux la méthode maintenant

merci

j'ai vu le message depuis longtemps mais je n'avais pas eu le temps de répondre

Posté par re : Cohérence spatiale - trou d'Young 10-01-16 à 15:01

Bonjour,

Citation :
j'ai vu le message depuis longtemps mais je n'avais pas eu le temps de répondre

Pas de problème ! J'imagine sans difficulté que le travail ne manque pas !

Posté par re : Cohérence spatiale - trou d'Young 10-01-16 à 15:02

exact

Ce topic

Imprimer
Réduire / Agrandir
Pour plus d'options, connectez vous !
Fiches de physique

Fiches de physique - chimie

Rechercher

Espace membre

Zone membre

Pas de compte ?
Je m'inscris

Changer d'île

Cohérence spatiale - trou d'Young

Seuls les membres peuvent poster sur le forum !

Ce topic

Fiches de physique