Inscription / Connexion Nouveau Sujet
coefficient de frottement
bonjour,
j'ai une question a propos d'un exercice alors voila :
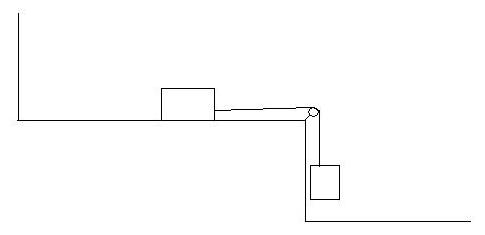
on a une masse M posée sur une table horizontale. elle est tirée par un fil inextensible de masse négligeable qui passe par une poulie a l'autre bout du fil est accroché une masse m
a t=O on lache le mobile sans vitesse initiale
a t1 la masse m touche le sol puis la masse M parcours encore une distance D avant de s'areter a t2
je n'arrive pas a répondre je crois que je raisonne mal
exprimer la vitesse v de la masse M au moment ou la masse m touche le sol
voila je pensais faire a l'instant x ou la masse m touche le sol, la masse M est a un point x
on a donc
position de M : x ux
vitesse de M : dx/ ux
mais ça me parait bizarre...
voila pouvez vous m'aider svp ?
merci
cordialement
akirasilver
il faut utiliser le théoreme de l'énergie cinétique d'abors a M puis pour se débarrasser de la tension T l'appliquer a la masse m
mais je n'y arrive pas
pouvez vous m'aider svp ?
merci
Je suppose qu'il faut prendre en compte les frottements dont tu n'as pas parlé pour l'instant...
On peut remarquer que, tant que le fil reste tendu, la variation de hauteur de la masse correspond à une variation identique de la position horizontale de la masse
.
Quel est le travail de la tension sur la masse ? Quel est le travail de la tension sur la masse
?
Quelles autres forces s'exercent sur le système? Que vaut leur travail respectif?
Il te faut répondre à ces questions avant de pouvoir appliquer le théorème de l'énergie cinétique.
la poulie est sans frottements
on cherche a déterminer le coefficient de frottement dynamique
la tension pour M et pour m est la meme
on a la variation d'energie cinétique qui vaut le travail des forces sur le chemin considéré.
on prend 0 au milieu de la poulie
l'axe x est en direction de M
l'axe Z en direction de m
donc L (longueur du fil) = x+z
pour M le bilan des forces est
T + P + Rn = Ma
or P+Rn = 0
on a donc
T = Ma
on calcule le travail de la tension en M
on a
dW = T.dx
pour m
on a W(T) + W(P)
W(T) =  T.dZ
T.dZ
W(P) =  P.dZ
P.dZ
= mgh
voila
C'est un peu confus.
On peut déjà voir qu'en effet le poids de est compensé par la réaction normale de la table et que globalement ces deux forces ne travaillent pas. On les oublie donc.
La masse est, elle, soumise à son poids dont le travail est effectivement donnée par
où
est la hauteur parcourue par m avant de toucher le sol. Ça c'est bon.
Mais n'oublies-tu pas les frottements dynamiques dans le bilan des forces s'exerçant sur ? Leur amplitude vaut
(Loi de Coulomb) et ils sont orientés de telle sorte qu'ils s'opposent au mouvement. Si je comprends bien ton exercice, le coefficient
est pour l'instant inconnu.
Sachant cela, que vaut le travail des forces de frottement sur la masse lorsque la masse m chute d'une hauteur
?
Remarque aussi que la tension exercée par la corde sur a la même valeur que celle s'exerçant sur
. En revanche la première est orientée dans le sens du mouvement de
, tandis que la seconde est orientée dans le sens inverse du mouvement de
. Si les deux masses parcourent une même distance, que peut-on dire du travail global de la tension sur les deux masses?
Pour résumer:
-travail de la tension sur les masses et
?
-travail des forces de frottement sur ?
Après ça, tu peux appliquer tranquillement le théorème de l'énergie cinétique au système "masse + masse
".
Comme cela a été dit, il manque des données sur le frottement.
Soit k (k dans ]0 ; 1[) le coefficient de frottement dynamique entre M et le support horizontal.
Travail du poids de la masse m qui descend d'une hauteur h : WP = mgh
Travail de forces de frottements entre M et le support au moment où m arrive au sol : Wf = -k.Mgh
Energie cinétique de m à l'arrivée au sol : Ec1 = (1/2).m.v² (avec v la vitesse de m juste avant l'arrivée au sol)
Energie cinétique de M à l'arrivée au sol de m : Ec2 = (1/2).M.v²
Bilan énergétique au moment où m arrive au sol :
mgh - k.Mgh = (1/2).m.v² + (1/2).M.v²
En connaissant g, m , M , h et k, on peut donc calculer v, la vitesse de M à l'arrivée de m au sol.
On peut donc en déduire l'énergie cinétique de M à cet instant.
... Et cette énergie cinétique se dissipera en chaleur par le travail de frottement entre le support et M qui continue à glisser.
La force de frottement est F = -k.M.g sur tout ce trajet.
La distance "d" de glissement de M (après que m soit arrivé au sol) est donc trouvé par (1/2).M.v² = k.M.g * d
Sauf distraction. 
les deux tensions s'annulent ? c'est pour ça qu'il faut appliquer deux fois le théoreme de l'energie cinétique
effectivement j'ai oublié cette partie dans le bilan et c'est assez embetant parce que tout ce que j'ai fait (bien que ce soit incomplet) est faux
donc je recommence :
travail de la tension sur les masses m et M s'annulent car on a T sur M et T sur m de meme valeur mais de sens opposé
on a pour le travail des forces de frottement sur M
W(Rn)+W(Rt)+W(P)
merci beaucoup pour toutes ces réponses ^^ je suis trop bete je fais un exercice sur les frottement et j'oublie de les exprimer T___T
enfin voila maintenant je dois en appliquant encore une fois le théoreme de l'éenrgie cinétique entre deux instants bien choisis, je dois trouver une relation entre les masses, fd, d et h puis en déduire fd
avec d = la distance parcourue par M apres l'arret de la masse m (au sol)
je choisi les instants soit t1 la masse m touche le sol et t2 la masse M s'arrete apres avoir parcouru une distance d
j'applique donc le théoreme de l'énergie cinétique entre t1 et t2 j'ai donc
Wtotal = W(P)+ W(fd)
W tot = Ec(t2)-Ec(t1)
j'ai donc
Ec(t2) = 0 car a t2 m est au sol depuis longtemps
Ec(t1) = 1/2M v²
par contre je ne sais pas comment sortir d
est ce que c'est correct ?
merci si vous pouvez m'aider
cordialement
akirasilver
Oui, sauf que le poids ne travaille pas.
Il te faut simplement exprimer le travail des forces de frottement sur la distance d.
Oui c'est ça.
Après il ne te reste plus qu'à remplacer par l'expression trouvée à la question précédente pour en déduire la valeur de
.
j'ai juste une question , je ne sais pas ce que représente d dans mon calcul, j'aurais dit Wf = -k.Mgh
mais je ne suis pas sure
merci beaucoup de m'aider autant
Apparemment, ton exercice utilise la notation pour le coefficient de frottement.
Pour la première partie où la masse chute, la masse
parcourt une distance
.
On a donc effectivement .
Pour la seconde partie ou seule la masse continue de se mouvoir, on te dit qu'elle parcourt une distance
avant de s'arrêter.
Le travail des forces de frottement vaut donc cette fois, non?
a oui c'est vrai j'ai repris la notation sans faire attention au changement
merci beaucoup j'aurais écris une bétise ^^
merci beaucoup d'avoir accordé du temps a mon probleme
cordialement
akirasilver
Le seul travail moteur dans l'exercice est celui de la masse m pendant sa descente: W1 = mgh
Le travail qui a accéléré les masses est W1 - k.M.g.h = mgh - k.Mgh (avec k le coeff de frottement dynamique de M sur son support).
La part de ce travail qui a été transmise à M penadnt la descente de m est : W2 = M/(m+M) * W1 = M/(m+M) * (mgh - k.Mgh)
Le travail de frottement de M sur son support apès impact de m au sol est donc = M/(m+M) * (mgh - k.Mgh)
On a alors immédiatement : M/(m+M) * (mgh - k.Mgh) = k.M.g.d
1/(m+M) * (mh - k.Mh) = k.d
mh = k.M.h + k.d.(m+M)
Et voila, en connaissant m, M et h :
Si on connait d on peut calculer k et si on connait k on peut calculer d.
-----
Sauf distraction. 


