Niveau licence

Clothoïde

Posté par
Mohamed1999 04-03-19 à 21:46

Salut,
j'ai un petit problème dans la courbe Clothoïde,je vais commencer par la définition pour être plus claire:
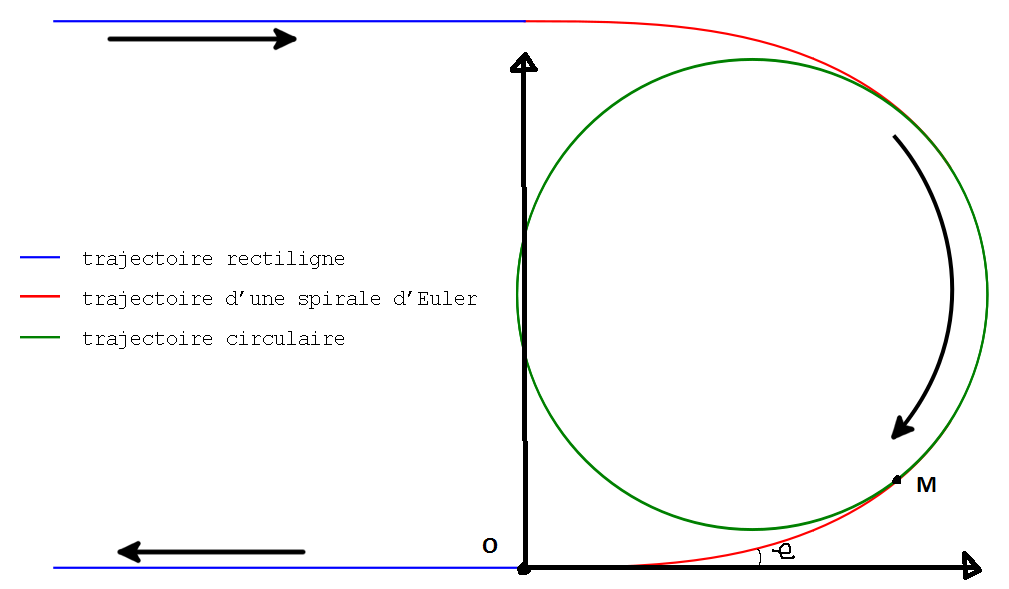
La clothoïde est une courbe utilisée sur les routes et les voies de chemin de fer pour raccorder une droite à un cercle (de Rayon R).

Ennoncé:
On prend l'origine des temps au début de la clothoïde. Soit L la longueur curviligne de la courbe L et t le temps mis pour parcourir L = OM.
Comme la vitesse est constante, on a : V = dL / dt.
Soit φ l'angle de la tangente à la courbe.
On modifie l'angle de braquage ω = dφ / dt de façon linéaire donc dω / dt = d²φ/dt² = Constante.
Comme dL / dt est aussi une constante, on a d²φ / dL² = Constante.

Mon problème:
1- Pourquoi d²φ / dL² = Constante .
2- Pourquoi il sont appelé ω = dφ / dt l'angle de braquage, normalement c'est la vitesse angulaire.
Merci.

Clothoïde

Posté par re : Clothoïde 04-03-19 à 22:26

Bonjour

Il s'agit je pense juste d'un problème de dérivée de « fonction composée » comme on dit.

Puisque : $v=\dfrac{dL}{dt}=constante$ :

$\dfrac{d\varphi}{dt}=\dfrac{d\varphi}{dL}\cdot\dfrac{dL}{dt}=v\cdot\dfrac{d\varphi}{dL}$

On dérive à nouveau par rapport à t :

$\dfrac{d^{2}\varphi}{dt^{2}}=\dfrac{d}{dt}\left(\dfrac{d\varphi}{dt}\right)=\dfrac{d}{dt}\left(v\cdot\dfrac{d\varphi}{dL}\right)=v\cdot\dfrac{d}{dt}\left(\dfrac{d\varphi}{dL}\right)=v\cdot\dfrac{d^{2}\varphi}{dL^{2}}\cdot\dfrac{dL}{dt}$

soit :

$\dfrac{d^{2}\varphi}{dt^{2}}=v^{2}\cdot\dfrac{d^{2}\varphi}{dL^{2}}$

L'utilisation de la lettre $\omega$ ici n'est pas très judicieuse car il ne s'agit nullement de la vitesse angulaire du véhicule. C'est la dérivée par rapport à t de l'angle $\varphi$ entre l'axe (Ox) et la tangente à la trajectoire. Cet angle $\varphi$ est aussi l'angle entre l'axe (Ox) et la direction du vecteur vitesse du véhicule en mouvement.