Voici le montage pour mieu voir et le sujet

L'autre partie si je n'ai pas été claire

** image supprimée **

Bonsoir
Il faut commencer par déterminer l'impédance complexe de l'association C//L. L'impédance complexe du circuit s'obtient en ajoutant R à cette expression.
L'intensité s'annule pour une pulsation particulière telle que le module de l'impédance complexe tend vers l'infini.
Je ne vois pas trop comment tu as pu faire la suite en partant d'une expression fausse de l'impédance complexe du circuit !

Oui c'est faut je rectifie ! J'obtiens
I= U / (jCw + 1/Lwj + R) à la question 1 désolé

Pour la question 2 je ne vois pas comment procéder , dois je faire tendre le module l'amplitude complexe vers l'infini puis observer qu'elle est la valeur obtenue ?

Bonjour à vous deux,

J'ai recadré la première image et supprimé la deuxième en vertu de la FAQ du forum :

extrait de la FAQ du forum :

Q05 - Puis-je insérer une image dans mon message ? Comment faire ? Quelle image est autorisée ?

Vous souhaitez ajouter une image ou un pdf à votre message . Veuillez obligatoirement respecter ces règles :

Énoncé d'exercice ou de problème :

Pour les énoncés courts (moins de 5 lignes sur une feuille A4) :
La recopie est obligatoire.
L'option d'attachement d'image n'est donc à utiliser que pour représenter une figure, un tableau ou un graphique, pas du texte !

Pour les énoncés longs  :
Les 5 premières lignes sont à recopier pour aider l'archivage des sujets sur le site.
Cela fait, l'énoncé dans sa totalité, pourra alors être joint en image (choisir Img) ou en pdf (choisir Pdf ) mais dans le respect des droits d'auteurs en vigueur. Pour les pdf, merci d'en préciser la source.

Recherches (même non abouties) de l'exercice :
Elles doivent être obligatoirement recopiées, et ce, dès la demande d'aide.
L'option d'attachement d'image n'est donc à utiliser que pour représenter une figure, un tableau ou un graphique, pas du texte !
Les formats autorisés sont exclusivement les suivants : gif, jpg, jpeg, et png. La taille d'un fichier est limitée à 2 MO maximum pour une image et à 500 ko pour un pdf.

Le non respect de ces règles entraînera la suppression du contenu de votre sujet (même si des réponses ont été apportées) et éventuellement la suspension de votre compte !

Bonjour gbm et bonne année 2019 !
Bonjour Aras
Ton expression de l'impédance complexe est toujours fausse. Il faut absolument que tu revois ton cours sur les associations de dipôles en série et en parallèle !

L'impédance de l'association L//C a pour expression :



L'impédance du circuit a donc pour expression :


Pour la question 2 : il faut effectivement se demander ce que devient la valeur du module de l'impédance complexe quand et quand 0.

Bonjour
Merci Bonne année 2019 Gbm!

D'accord c'est que dans mon cour il est dis que dans une association en parallèle , les dipôles voient leur admittance (1/z) s'ajouter et donc j'ai laisser 1/JLwet JCw.

Enfin bon avec la forme que vous m'avez proposée je ne peux pq mettre sous forme canonique car après je doit remplacer L/Rwo=Q et la je ne vois pas comment isoler le R pour faire apparaître le Q

Donc l'amplitude complexe serait de la forme I=U/(R - j(Lw/LCw^2-1)
J'isole R pour mettre sous forme canonique I= U/(R(1-j((Lw)/LCRw^2-R) et à partir de la mettre sous forme canonique avec Q=R/Lwo  je n'y arrive pas

Si :



alors :



J'espère que tu as compris maintenant...
Pour un très grand débutant en électrocinétique, tu abordes peut-être un sujet un peu difficile. Tu t'acharnes à faire intervenir Q alors que cela n'est utile qu'à partir de la question 4 comme le précise clairement l'énoncé et tu en es toujours à la première question ! L'expression de Z que je t'ai fournie est la plus pratique pour répondre aux trois premières questions. Ensuite il faut la modifier un peu : l'astuce consiste à mettre R en facteur mais la question est prématurée puisque tu n'a pas encore démontré l'expression de _o. Pour résoudre la question 4, il faut faire intervenir Q mais aussi le rapport (/_o) ...
Attention aussi à ne pas confondre l'impédance complexe et son module...

D'accord merci j'ai compris !!

Si je m'acharne à faire apparaître Q et le rapport w/w0 c'est que je pensais en avoir besoin deja pour la question 3 pour trouver Imax et remplacé le rapport w/w0 par x pour passer par une étude de fonction mais bon je dois m'y prendre trop tot peut être

Je vous remercie de votre aide et votre temps car il m'est très utile d'autant plus que j'aimerai comprendre cette exo
Merci encore

Donc pour la question 1 on  I=E/(R-jLw/LCw^2-1)

Pour la question 2 Le module de I (amplitude complexe) vaut E/sqrt(R^2+(-Lw/(LCw^2-1)^2
Donc l'impedence complexe vaut sqrt(R^2+(Lw/LCw^2-1)^2 je dois maintenant faire tendre Omega vers l'infini et 0

D'accord avec ton expression du module de l'impédance complexe. Tu peux alors remarquer que, si LC²1, le module de Z tends vers l'infini, donc la valeur efficace de l'intensité tend vers zéro. Cela va te fournir la valeur de _o. Pour la question 4, tu auras tout intérêt à poser, après la mise en facteur dont je t'ai parlée :

et
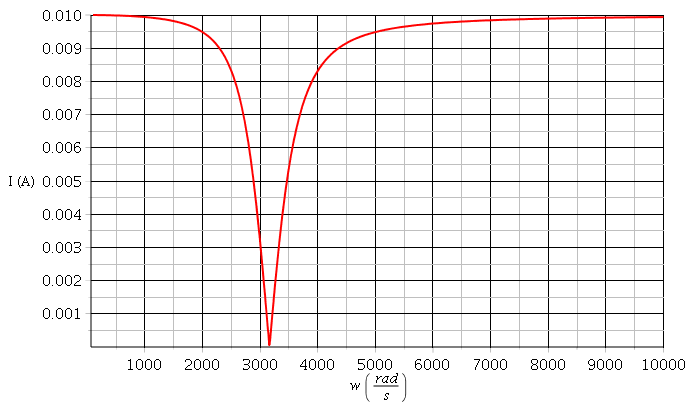
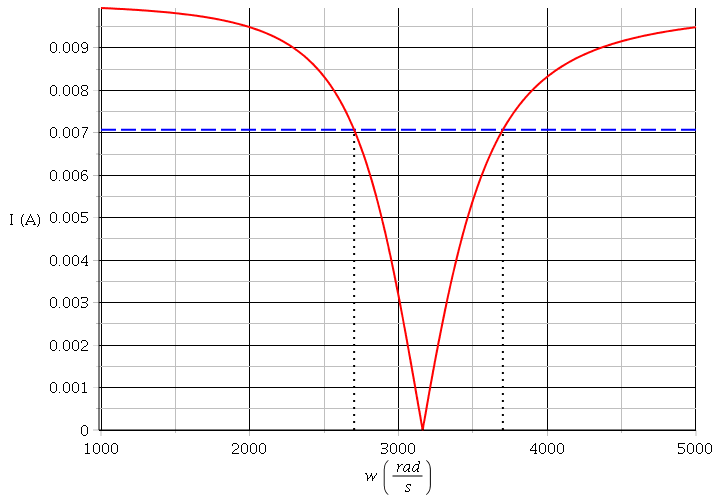
Pour t'aider un peu, je te fournis la courbe I=f() en choisissant arbitrairement E=10V. pour la première courbe, j'ai choisie une échelle étendue permettant de bien visualiser les asymptotes horizontales. Dans le second cas, j'ai resserré l'échelle autour de la valeur _o. J'ai tracé en pointillé l'horizontale correspondant à Imax/2 et j'ai tracé en pointillé les verticales d'abscisses ₁ et ₂.

Je ne comprends pas tellement la différence entre là questions 2 et 3 car à la question 3 je dois aussi faire tendre Omega pour trouver Imax

Enfait je n'ai pas compris le raisonnement de la question 2 car quand LCw^2 ->1 et bien on a l'imprudence qui tend vers R pour moi car
Sqrt(R^2+(Lw/1-1) sa fait sqrt(R^2)

Je dois sûrement faire une bêtise mais j'aimerai comprendre

Que vaut selon toi la limite de quand :

1° :

2° :

3° : ???

Pour moi
1- la limite vaut R
2-elle vaut + infini
3-forme indéterminé +infini/+infini

Je crois qu'il faut aussi que tu revois ton cours de math.
Tout est faux :
1° Ajouter R² à un terme qui tend vers l'infini donne une expression qui tend vers l'infini.
2° le terme qui dépend de tend vers zéro ; l'impédance tend vers R
3° comme pour 2°...

Mais si LCw^2 tend vers 1  alors Lw/1-1 tend vers 0 alala je penses que je fais n'importe quoi

Pour le terme qui dépend de quand LC²1 :
le dénominateur tend vers zéro alors que le numérateur tend vers une valeur non nulle qu'il n'est pas nécessaire de calculer. Cela suffit pour dire que l'expression tend vers l'infini.

D'accord merci beaucoup je comprend mieux

Mais quelle est la finalité de ces calculs de limite ?

Je ne comprends pas bien cette phrase "le module de Z tends vers l'infini, donc la valeur efficace de l'intensité tend vers zéro. Cela va te fournir la valeur de w0"

est la valeur particulière de la pulsation telle que , donc

. Franchement... Tu es vraiment en math sup ?

Non j'aimerai y aller l'année prochaine donc je m'avance cette année quand je parles de cour c'est ce que des amis me font par j'ai du mal oui c'est vrai...  

Sinon merci beaucoup donc pour la question 2 on a la valeur de w0 je la connaissais sans savoir la démontrer maintenant je sais merci

Pour la question 3 pour trouver Imax besoin de faire une dérivation pour savoir pour quelle valeure de Omega il est atteind n'est ce pas ?

Ou alors dois je faire encore tendre w vers 0 et l'infini suivant l'amplitude complexe ?

Imax = E/R lorsque w tend vers 0 et l'infini ?

Aidez moi svp j'aimerai bien finir cette exo aujourd'hui

D'accord merci

Pour la question 4, j'ai isolé R j'ai donc I=E/(R(1-Lw/R/LCw^2-1)

À partir de la je dois faire apparaître Q=R/Lw0 et le rapport w/w0 donc j'ai donc fais comme vous avez proposé et remplacé LCw^2 par (w/w0)^2 mais je n'aboutit à rien de concret

J'aboutit a (1/Q^2)(w/wo)^2/((w/Wo)^2-1)^2=1

Oui d'accord merci

Ensuite pour trouver w1 et w2 je prend l'expression à laquelle j'ai aboutir (1/Q^2)(w/wo)^2/((w/Wo)^2-1)^2=1
Mais je ne sais pas comment faire apparaître une équation du 2nd ordre pour trouver trouver w1 et w2

J'ai donc (w/wo)^2/((w/Wo)^2-1)^2-Q^2=0 oui je fais (w/wo)^2/((w/Wo)^2-1)^2-Q^2
=((w/wo)/((w/Wo)^2-1)-Q)*((w/wo)/((w/Wo)^2-1)+Q)=0
Donc soit (w/wo)/((w/Wo)^2-1)-Q=0 soit (w/wo)/((w/Wo)^2-1)+Q=0

Mais à partir de la je ne m'en sors plus j'ai peut être fait une erreur de calcul mais je ne trouves pas

En posant, pour alléger les notations :



le problème revient à trouver les deux valeurs de x, l'une comprise entre 0 et 1, l'autre supérieure à 1, telles que :



il faut envisager deux cas :

1° :

2° :
Chaque cas correspond mathématiquement à deux valeurs de x : une positive, l'autre négative ; seule la valeur positive a un sens physique. Tu vas donc ainsi obtenir les deux valeurs recherchées.

D'accord merci beaucoup pour votre aide ca m'a beaucoup éclairé sur plusieurs points de sujet
Pour terminer, afin de déterminer les valeurs de ic(t) et iL(t)  doit on passer par une loi des mailles ? Et sachant sinon ne connait pas la valeure de E doit on en prendre une arbitrairement ?

Pour la dernière question, sachant que l'intensité du courant principal (celui traversant R et le générateur) est nulle, la tension aux bornes de R est nulle à chaque instant, de sorte quela tension commune aux bornes de L et C est la tension e délivrée par le générateur. En raisonnant sur les complexes associés, cela conduit simplement à :



puisque : dans ce cas particulier du fonctionnement en circuit bouchon.

Tu vas obtenir deux intensités de même valeur maximale (amplitude), de même période mais en opposition de phase. Leur somme est nulle à chaque instant.
Ton problème demande peut-être seulement un résultat littéral mais le fait de ne pas avoir fourni de valeur numérique à E est peut-être une étourderie du concepteur du problème. Pour les courbes précédente, j'avais choisi arbitrairement une valeur efficace E=10V.

D'accord merci donc je remplace e par Ecos(wt+phi) et doit on passer par le module et l'argument pour avoir iCet iL réelles ?

D'accord donc à la fin de mes calculs
j'ai iC=CwE(wt+pi/2)
Et iL=-CwE(wt+pi/2)
Est ce correct ?
Ou alors iL=E/Lw*cos(wt-pi/2) ?

Enfin w remplacé par w0 dans mes expressions

remplacer /2 par -/2 est équivalent à changer le signe du cosinus. Compte tenue de la relation entre C_o et , tes deux expressions de i_L sont équivalentes.

En faisant les applications numériques j'obtiens des valeurs négatives ? Est ce normal ou est ce lié au phénomène de surcourant ? Ou me suis je trompé ?

J'en obtiens une positive et une négative et donc en les additionnant elles vont s'annuler d'où le phénomène de surcourznt je penses

Non je me suis trompé dsl