Inscription / Connexion Nouveau Sujet
Circuit RLC parallèle.
Bonsoir 
,
J'aurais besoin d'un peu aide sur un exo d'entrainement en vue d'un prochain DS.
Parfois j'y arrive, parfois je ne vois pas trop alors j'essaie d'élargir mon pannel d'exercices..
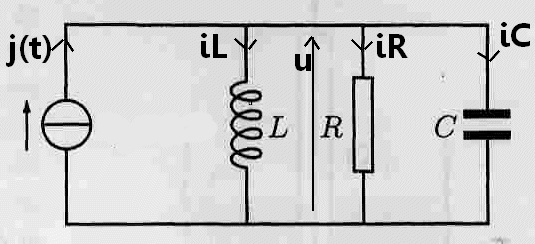
Bref, voici l'exo :
À t<0, j(t)=J et à t>0, j(t)=0
R=470
- Déterminer les valeurs de iL, iR, iC et u à t(0+) et t(0-).
- Etablir à l'aide des lois de Kirchoff, l'équation différentielle satisfaite par le courant iL à t>0.
- En déduire que u vérifie :
d2u/dt2+1/RC x du/dt + 1/LC x u = 0
- Définir alors en fonction de R,L et C le facteur de qualité Q, la pulsation propre 
0 et le coefficient d'amortissement 
du circuit.
- En sachant que le régime est pseudo-sinusoïdal, démontrez que pour tout t
0, u(t)=-J/Csin(t)exp(-t)
On exprimera en fonction des autres données.
Pour l'instant j'ai dit que :
À t<0, les transitoires ont eu un temps infini pour disparaitre donc on se trouve en régime continu. De plus, le condensateur est alors semblable à un interrupteur ouvert et iC(0-) = 0
On a donc j=iR+iL avec iR=u/R et u = LdiL/dt = R x iR = q/c
Je sais aussi que l'intensité circulant dans une bobine est une fonction continue du temps donc on aura iL(0-)=iL(0+) = ?
Est-il nécessaire que j'utilise l'équivalence Thévenin-Norton ou alors est-ce mieux de laisser le circuit ainsi et d'appliquer loi des noeuds / lois des mailles directement ?
Merci de me guider un peu dans cet exercice
Et voilà le circuit :
Edit Coll : image placée sur le serveur de l' 
Merci d'en faire autant la prochaine fois ! 
Salut
1) en régime permanent, la bobine se comporte comme un fil et la condensateur comme un interrupteur ouvert. Donc iL(t=0-)=iL(t=0+)=J (court circuit de la résistance).
iR(t=0-) = 0 puisqu'il y a court-circuit
iC(t=0-) = 0 puisque le condo se comporte cmme un interrupteur ouvert.
A t=0+, j(t) = 0 et iL = J donc il faut iR+iC = -J
Ah ! Merci beaucoup, je n'avais pas du tout pensé au court-circuit de la résistance mais c'est vrai que j'aurais du !
Pour u on peut dire que u = LdiL/dt = R x iR
donc u(0-) = 0 car iL = constante donc dérivée = 0, et iR = 0.
u(0+) = 0 à priori puisque iL = constante, non ?
Par contre lorsqu'on dit iR+iC = -J, comment est-ce qu'on peut séparer iR et iC ?
Désolée pour le double post..
J'ai trouvé ! Enfin je pense : u(0+)=0 car iL(0+) constante, donc nécessairement iR(0+)xR = 0 et iR(0+)=0. Et iC(0+)=-J.
Pour la seconde, faut-il que je transforme en Thévenin ou comme ça c'est bon ?
u(0+)=0 en effet par continuité de la tension aux bornes du condensateur. Donc iR(0+)=0 par la loi d'ohm. D'où iC(0+)=-J
Annuler
connectez vous