Circuit RLC - Fonction de transfert / Gain - forum physique chimie

 Niveau licencePartager :
			        
Circuit RLC - Fonction de transfert / Gain
Posté par 
pegoud  10-03-21 à 17:20
Bonjour,

J'ai prochainement un TP de Physique portant sur les circuits RLC, et j'aurais besoin de quelques éclaircissements si quelqu'un se sent l'âme de m'aider 

Ma préparation de TP commence ainsi :

Montrer que, si r = 0, la fonction de transfert H(jω) est donnée par :

H(jω) = 

En déduire le gain en tension G(ω).

Je ne maîtrise pas vraiment ces notions et je ne sais pas par où commencer cette petite démonstration.

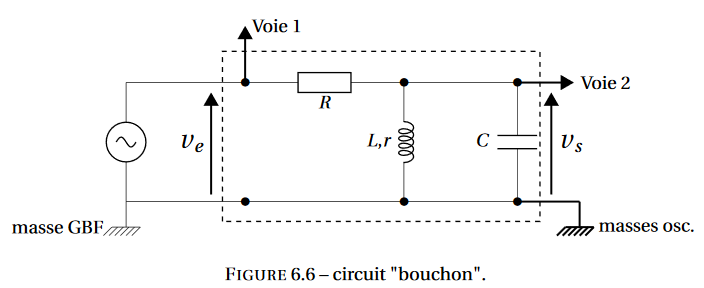
Si besoin, j'ai disposé en annexe le circuit bouchon en question.

Merci d'avance !

 Posté par 
vanoisere : Circuit RLC - Fonction de transfert / Gain  10-03-21 à 17:27
Bonjour

Commence par remplacer( L,r//C) par son impédance équivalente complexe puis utilise la notion de diviseur de tension.
 Posté par 
pegoudre : Circuit RLC - Fonction de transfert / Gain  10-03-21 à 17:38
Merci ! Je vais essayer de faire ça et je vous réponds si je trouve 
 Posté par 
pegoudre : Circuit RLC - Fonction de transfert / Gain  10-03-21 à 17:49
Je ne sais pas si c'est correct, mais je trouve :

zL,r = zL + zr = jLω + r

et

zC = 1/jωC

Si c'est juste, je trouve l'impédance équivalente suivante :

Zéq = [r+jLω]/[jω(Cr+L)+1] 
 Posté par 
vanoisere : Circuit RLC - Fonction de transfert / Gain  10-03-21 à 18:13
Ton résultat est nécessairement faux car il n'est pas homogène : L est une inductance, r.C est homogène à un temps : il n'est pas possible physiquement de faire la somme de deux grandeurs n'ayant pas la même dimension physique.

Quelle est L'expression de Zeq en fonction de ZLr et de Zc ?

Reprends ton calcul en vérifiant bien l'homogénéité du résultat.
 Posté par 
vanoisere : Circuit RLC - Fonction de transfert / Gain  10-03-21 à 18:43
Tu peux d'entrée poser r= 0 pour ce calcul. Cela va simplifier la situation.
 Posté par 
pegoudre : Circuit RLC - Fonction de transfert / Gain  10-03-21 à 18:44
J'avais noté que :

Zéq = ZLr.ZC/ZLr+ZC

Si cette expression de base est juste, alors j'ai dû faire une erreur dans le développement... 
 Posté par 
pegoudre : Circuit RLC - Fonction de transfert / Gain  10-03-21 à 18:45
Nos messages se sont croisés, je l'ai bien reçu merci !
 Posté par 
vanoisere : Circuit RLC - Fonction de transfert / Gain  10-03-21 à 18:59
D'accord avec ton message de 18h44. 
 Posté par 
pegoudre : Circuit RLC - Fonction de transfert / Gain  10-03-21 à 19:00
J'ai posé r = 0 comme vous me l'avez suggéré.

Je trouve ce résultat :

Zéq = (Ljω)/(-LCω²+1)
 Posté par 
pegoudre : Circuit RLC - Fonction de transfert / Gain  10-03-21 à 19:15
Si ce résultat est correct, vous m'avez proposé d'utiliser la notion de diviseur de tension... mais je ne sais pas vraiment quelle formule utiliser.

Si vous avez encore un peu de temps, pourriez-vous éclairer ma lanterne ? Merci d'avance !
 Posté par 
vanoisere : Circuit RLC - Fonction de transfert / Gain  10-03-21 à 19:23
On peut considérer R et le dipôle équivalent d'impédance Zeq comme parcourus par le même courant ; donc :

 Posté par 
pegoudre : Circuit RLC - Fonction de transfert / Gain  10-03-21 à 19:39
Merci beaucoup ! 

Après plusieurs manipulations, j'ai finalement réussi 

La question suivante concerne la déduction du gain en tension G(ω).

Je sais que cela correspond au module de H : je le calcule de suite.
 Posté par 
pegoudre : Circuit RLC - Fonction de transfert / Gain  10-03-21 à 19:57
Je reviens vers vous, je viens de calculer le gain.

J'ai trouvé que :

G = 

Est-ce que ça vous paraît plausible ?

Je suis censé en déduire une valeur de ω0.
 Posté par 
vanoisere : Circuit RLC - Fonction de transfert / Gain  10-03-21 à 20:10
Une façon simple d'obtenir le module de la fonction de transfert complexe :

Tu obtiens le module comme la racine carrée du produit de la fonction de transfert par son conjugué.

Si tu n'es pas très à l'aise avec l'utilisation des nombres complexes pour l'étude des circuits en régime sinusoïdal, tu peux consulter la fiche suivante, partie 1. Les parties 2 et 3 ne sont pas à ton programme pour l'instant.

 Posté par 
pegoudre : Circuit RLC - Fonction de transfert / Gain  10-03-21 à 20:20
Merci beaucoup une nouvelle fois !

Je consulte tout ça et j'essaye de faire le calcul.
 Posté par 
pegoudre : Circuit RLC - Fonction de transfert / Gain  10-03-21 à 20:49
J'ai essayé d'appliquer la formule et j'obtiens :

Je ne sais pas si ça correspond au résultat attendu... Sinon je ne vois pas comment faire.

(et je me rends compte que je n'ai pas réduit au même dénominateur)
 Posté par 
pegoudre : Circuit RLC - Fonction de transfert / Gain  10-03-21 à 20:52
... d'autant qu'il faut que j'introduise le fameux ω0.
 Posté par 
pegoudre : Circuit RLC - Fonction de transfert / Gain  10-03-21 à 21:18
Après avoir simplifié l'expression, je trouve finalement :

Si cette expression est cohérente, dois-je considérer que ω0 = 1/RC ?
  Posté par 
pegoudre : Circuit RLC - Fonction de transfert / Gain  10-03-21 à 21:42
Oubliez ce que je viens de dire !

J'ai fini par comprendre (il a fallu le temps  )

D'après la dernière expression, j'ai trouvé que le gain était maximal pour ω0² = 1/LC.

En tout cas, encore un immense merci pour vos précieuses indications,

Je vous souhaite une bonne soirée !